Question

A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are respectively ${30^0}$ and ${60^0}$.Find the height of the tower.

Answer 1

Hint- Draw the diagram of question and use value of trigonometric angles $\tan {30^0} =
 \frac{1}{{\sqrt 3 }}$ and $\tan {60^0} = \sqrt 3 $ .

Let QR be the height of the tower (h meters) and RS be the height of flagstaff surmounted on
 the tower (RS=5m). Let the point P lie on the horizontal plane at a distance of x meters from
 the foot of the tower at point Q (PQ=x meters).

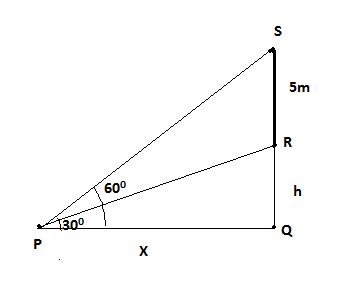
In $\vartriangle PQR$, the angle of elevation of the bottom of the flagstaff is ${30^0}$ .
$
  \tan {30^0} = \dfrac{{QR}}{{PQ}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \frac{h}{x} \\
   \Rightarrow x = \sqrt 3 h.........\left( 1 \right) \\
 $
In $\vartriangle PQS$, angle of elevation of the top of the flagstaff is ${60^0}$ .
$
  \tan {60^0} = \dfrac{{QS}}{{PQ}} = \dfrac{{QR + RS}}{{PQ}} \\
   \Rightarrow \sqrt 3 = \dfrac{{h + 5}}{x} \\
   \Rightarrow x = \dfrac{{h + 5}}{{\sqrt 3 }}..........\left( 2 \right) \\
 $
Eliminating x using (1) and (2) equation
$
   \Rightarrow \sqrt 3 h = \dfrac{{h + 5}}{{\sqrt 3 }} \\
   \Rightarrow 3h = h + 5 \\
   \Rightarrow 2h = 5 \\
   \Rightarrow h = 2.5m \\
$
So, the height of tower is 2.5 meters

Note- Whenever we face such types of problems we use some important points. Like draw
 the figure of question with notify all points and distances then make the relation between
 variables with the help of trigonometric angles then after eliminating x we can get the value
 of the height of the tower.