Question

A tower subtends a right angle at the top of the hillock and the angle of elevation of the top of the hillock from the bottom of the tower is 60°. If the distance between the tower and the hillock is 6 m, then the height of the tower is
A. \[2\sqrt 3 \] m
B. \[4\sqrt 3 \]m
C. \[\sqrt 3 \] m
D. \[8\sqrt 3 \]m

Answer 1

Hint: Here, draw the figure which represents the statements given in questions geometrically. Draw perpendicular lines to form right-angled triangles. Apply trigonometrical tool tan 30° and tan 60° in right triangles to find the unknown sides, as these angles are given or we can find it geometrically. Find the height of the tower in two parts and add them to get the total height of the tower.

Complete step by step answer:

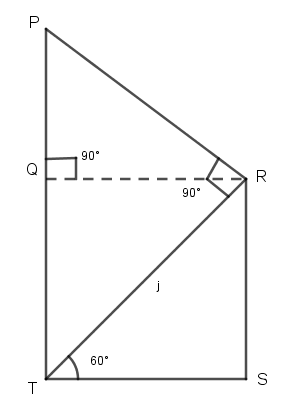
In the figure, let PT be the tower of height H and RS be the hillock of height h. As given tower subtends a right angle at the top of the hillock i.e. ∠PRT = 90° and the angle of elevation of the top of the hillock from the bottom of the tower is 60° i.e. ∠STR = 60°.
Draw QR parallel to TS.
From the figure, QT = RS
Also given the distance between tower and hillock is 6 m, therefore, QR = TS = 6 m.
As QR is parallel to TS and RT is transversal, ∠PRQ = ∠QRT [Alternate interior angles]
∠PRQ = ∠QRT = 60°
Given, ∠PRT = 90°
Therefore, ∠PRQ + ∠QRT = 90°
⇒ ∠PRQ = 90° − 60° = 30°
In right angled$\vartriangle PQR$
$\tan {30^ \circ } = \dfrac{{PQ}}{{QR}}$
[Since, for ∠PRQ, Perpendicular is PQ and Base is QR]
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{PQ}}{6}$
[Since, tan 30° = $\dfrac{1}{{\sqrt 3 }}$ and QR = 6 m]
$ \Rightarrow PQ = \dfrac{6}{{\sqrt 3 }} = 2\sqrt 3 $ … (i)
Now, in right angled$\vartriangle RST$
$\tan {60^ \circ } = \dfrac{{RS}}{{TS}}$
[Since, for ∠RTS, Perpendicular is RS and Base is TS]
$ \Rightarrow \sqrt 3 = \dfrac{{RS}}{6}$
[Since, tan 60° = $\sqrt 3 $ and TS = 6 m]
$ \Rightarrow RS = 6\sqrt 3 $ …(ii)
Now, PT = PQ + QT = $2\sqrt 3 + 6\sqrt 3 = 8\sqrt 3 $ [From equations (i) and (ii)]
Therefore, the height of the tower is $8\sqrt 3 $ units.
Hence, the option (D) is correct.
Note:
  In these types of questions always draw the correct figure based on the statements given in the question. If you do not draw the correct figure, it would be impossible to solve the question. There is neither any algebraic method to solve this question nor any alternative method which can solve without drawing a figure.