Question

A square circumscribes a circle and another square is inscribed in this circle with one vertex at the point of contact. The ratio of the areas of the circumscribed and inscribed squares is
A) 1:2
B) 2:1
C) 3:1
D) 4:1

Answer 1

Hint:
1) Angle in a semicircle is 90 degree
2) The length of the side of the square circumscribing a circle is equal to the diameter of the circle.
3) The length of diagonal of the square inscribing the circle is equal to the diameter of the circle.

Complete step by step solution:
As shown in figure, square ABCD circumscribes a circle having radius ‘r’ and another square EFGH is inscribed in that circle.

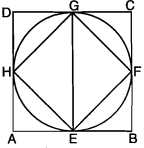
As GE is diameter of circle; $GE = 2r$
Then, \[\angle GHE = {90^0}\] (angle in a semicircle)
As EFGH is a square, so EF=FG=GH=HE as all sides of squares are equal.
Applying Pythagoras theorem in $\vartriangle GHE$; we get,
$G{E^2} = G{H^2} + H{E^2}$
As GE is diameter of circle (2r) and GH=HE (sides of square EFGH)
${(2r)^2} = G{H^2} + G{H^2}$
$4{r^2} = 2G{H^2}$
$G{H^2} = 2{r^2}$
Area of square EFGH = $G{H^2} = 2{r^2}$
As we see in diagram, $AD = GE = BC = 2r$
So, area of square ABCD= ${(2r)^2} = 4{r^2}$
Now, we have to find ratio of areas of circumscribed square and inscribed square:
$\dfrac{{ar(squareABCD)}}{{ar(squareEFGH)}} = \dfrac{{4{r^2}}}{{2{r^2}}} = 2$

So, ratio is 2:1 (option B is correct)

Note:
If a polygon is drawn in a circle so that every corner of the polygon lies on the circle, the polygon is called an inscribed polygon and the circle is called the circumscribed circle.
If all the vertices of a polygon A lies on sides of other polygon B, then polygon A is said to be inscribed in polygon B.