Question

A solid sphere of radius \[\dfrac{R}{2}\] is cut out of a solid sphere of radius R such that the spherical cavity on the other side is shown. The initial mass of the Solid sphere was M. If a particle of mass m is placed at a distance of \[\text{2}\text{.5R}\] from the centre of cavity then what is the gravitational attraction on the mass m?

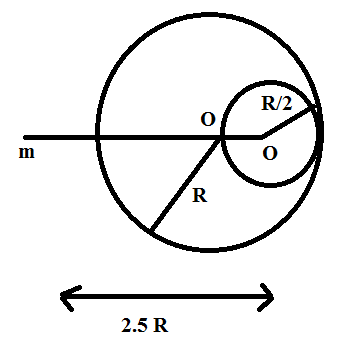
A. \[\dfrac{\text{GMm}}{{{\text{R}}^{\text{2}}}}\]
B. \[\dfrac{\text{GMm}}{\text{2}{{\text{R}}^{\text{2}}}}\]
C. \[\dfrac{\text{GMm}}{\text{8}{{\text{R}}^{\text{2}}}}\]
D. \[\dfrac{\text{23GMm}}{\text{100}{{\text{R}}^{\text{2}}}}\]

Answer 1

Hint: We have to apply Newton's law of gravitation here.
\[{{F}_{grav.}}=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{d}^{2}}}\]
\[{{m}_{1}}\]= mass of the object 1
\[{{m}_{2}}\] = mass of the object 2
D = distance separating them
G = Universal gravitational constant
G = \[\text{6}\text{.673 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-11}}}\text{ N}{{\text{m}}^{\text{2}}}\text{/k}{{\text{g}}^{\text{2}}}\]
We have to find the gravitational force on the particle when the spherical was not cut out and then we have to find the gravitational force on the find due to the cutout particle, sphere of radius \[\dfrac{R}{2}\]. Then subtract them with each other i.e. Force of gravitational due to radius 'R' Force of gravitation due to radius \[\dfrac{R}{2}\].

Complete step-by-step answer:
First we have to find the mass of the cavity.
Density of the sphere of radius 'R':
\[P=\dfrac{M}{V}\]
P= density
M = mass
V = Volume
Volume of the sphere \[=\dfrac{4}{3}\pi {{R}^{3}}\]
R= radius of the sphere.
\[P=\dfrac{M}{\dfrac{4}{3}\pi {{R}^{3}}}\]
Density remains the same even though the cavity is cut out.
Mass of the cavity of radius\[\dfrac{'R'}{2}=\dfrac{4}{3}\pi {{\left( \dfrac{R}{2} \right)}^{3}}\times P\]
\[\dfrac{4}{3}\pi {{\left( \dfrac{R}{2} \right)}^{3}}\times \dfrac{M}{\dfrac{4}{3}\pi {{R}^{3}}}\]
Mass of the cavity (M’) = \[\dfrac{M}{8}\]
.Force of gravitation on particle ‘m’ due to \[M:{{F}_{1}}=\dfrac{G\times m\times M}{{{d}^{2}}}\]
Distance between particle 'm' from the Centre of sphere of mass 'm' due to
 \[\text{ }\!\!'\!\!\text{ M }\!\!'\!\!\text{ =2}\text{.5R-0}\text{.5R}\]
\[d=2R\]
Substitute this d in \[{{F}_{1}}\]
\[{{F}_{1}}=\dfrac{G\times m\times M}{{{\left( 2R \right)}^{2}}}\Rightarrow {{F}_{1}}=\dfrac{GmM}{4{{R}^{2}}}\]
Force of gravitation on particle in due to the cavity of mass \[\dfrac{\text{ }\!\!'\!\!\text{ M }\!\!'\!\!\text{ }}{\text{8}}:-{{F}_{2}}=\dfrac{G\times m\times \dfrac{M}{8}}{{{d}^{2}}}\]
Here the distance between particle 'm' from the centre of the sphere of mass \[\dfrac{\text{ }\!\!'\!\!\text{ M }\!\!'\!\!\text{ }}{\text{8}}\Rightarrow {{d}_{1}}=2.5R\]
Substitute \[{{d}_{1}}\] in \[{{F}_{2}}\]
\[{{\text{F}}_{\text{2}}}\text{=}\dfrac{\text{G }\!\!\times\!\!\text{ m }\!\!\times\!\!\text{ }\dfrac{\text{M}}{\text{8}}}{{{\left( \text{2}\text{.5R} \right)}^{\text{2}}}}\]
If we \[{{F}_{1}}-{{F}_{2}}\] .then we will get the gravitational force on the particle 'm' when the part was cut ie, \[\dfrac{R}{2}\] radius part was cut from original Sphere.
\[{{\text{F}}_{\text{net}}}\text{=}{{\text{F}}_{1}}-{{\text{F}}_{\text{2}}}\]
\[{{\text{F}}_{\text{net}}}\text{=}\dfrac{\text{GMm}}{{{\text{R}}^{\text{2}}}}\text{-}\dfrac{\text{Gm }\!\!\times\!\!\text{ M}}{\text{8 }\!\!\times\!\!\text{ }\dfrac{\text{25}}{\text{4}}{{\text{R}}^{\text{2}}}}\]
\[{{\text{F}}_{\text{net}}}\text{=}\dfrac{\text{23}}{\text{100}}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{GMm}}{{{\text{R}}^{\text{2}}}}\].
Option (D) is correct.

Note: Newton's law of gravitation: It states that every particle attracts every other particle in the universe with a force that is directly proportional to product of their masses and inversely proportional to square of the distance between the centers.
\[F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
\[{{m}_{1}},{{m}_{2}}\] = mass of the objects
r = distance between their centre of masses
G = Universal gravitational constant.
Density is an intensive property. That's why regardless of the object size, shape or quantity