Question

A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone.

Answer 1

Hint – In this question first draw the pictorial representation of the problem it will give us a clear picture of what we have to find out later on apply the property of similar triangles and calculate the base radius of smaller cones, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

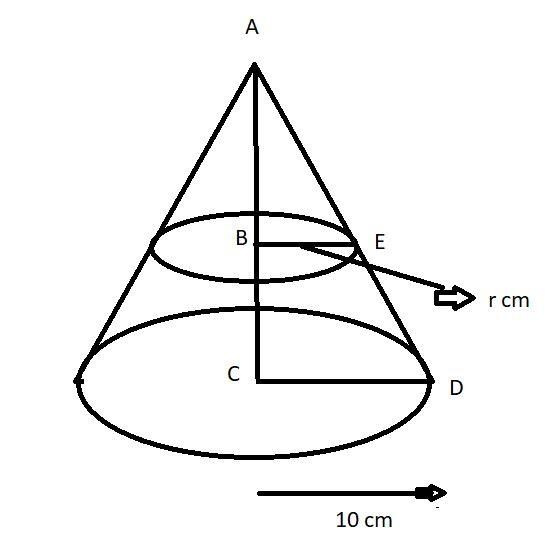
Let us consider the cone as shown in figure the base radius (R) of the cone is 10 cm (see figure.)
Now the cone cut into two parts through the midpoint of its height (at point B see figure).
Let the height of the cone be h cm.
$ \Rightarrow AB = BC = \dfrac{h}{2}$ cm.
Let the base radius of the smaller cone is r cm.
$ \Rightarrow BE = r$ cm (see figure).
Now the triangle ABE and the triangle ACD is concurrent by the property of angle-angle-angle (AAA).
$ \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CD}}$
Now substitute the values in above equation we have,
$ \Rightarrow \dfrac{{\dfrac{h}{2}}}{h} = \dfrac{r}{{10}}$
On simplifying we get.
$ \Rightarrow r = 5$ cm.
As we know that the volume of the cone is $ = \dfrac{1}{3}\pi {\left( {{\text{radius}}} \right)^2}\left( {{\text{height}}} \right)$
So the volume (${V_1}$) of the upper part of the bigger cone which is also a cone is
$ \Rightarrow {V_1} = \dfrac{1}{3}\pi {\left( {BE} \right)^2}\left( {AB} \right) = \dfrac{1}{3}\pi {\left( r \right)^2}\left( {\dfrac{h}{2}} \right)$…………………. (1)
Let the volume of the lower part is (${V_2}$) so the volume of the lower part is calculated as subtraction of volume of bigger cone and volume of smaller cone.
Volume (V) of bigger cone is $ = \dfrac{1}{3}\pi {\left( {{\text{radius}}} \right)^2}\left( {{\text{height}}} \right)$
$ \Rightarrow V = \dfrac{1}{3}\pi {\left( R \right)^2}h$
So the lower part volume is
$ \Rightarrow {V_2} = V - {V_1}$
$ \Rightarrow {V_2} = \dfrac{1}{3}\pi {\left( R \right)^2}h - \dfrac{1}{3}\pi {\left( r \right)^2}\left( {\dfrac{h}{2}} \right)$
So, the required ratio (RT) of two parts of the cone is
$ \Rightarrow RT = \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi {{\left( r \right)}^2}\left( {\dfrac{h}{2}} \right)}}{{\dfrac{1}{3}\pi {{\left( R \right)}^2}h - \dfrac{1}{3}\pi {{\left( r \right)}^2}\left( {\dfrac{h}{2}} \right)}}$
Now substitute the values in the above equation we have,
$ \Rightarrow RT = \dfrac{{\dfrac{1}{3}\pi {{\left( 5 \right)}^2}\left( {\dfrac{h}{2}} \right)}}{{\dfrac{1}{3}\pi {{\left( {10} \right)}^2}h - \dfrac{1}{3}\pi {{\left( 5 \right)}^2}\left( {\dfrac{h}{2}} \right)}}$
Now cancel out the common term $\dfrac{1}{3}\pi \left( {\dfrac{h}{2}} \right)$ from, numerator and denominator and simplify we have,
$ \Rightarrow RT = \dfrac{{{{\left( 5 \right)}^2}}}{{\left[ {2{{\left( {10} \right)}^2} - {5^2}} \right]}} = \dfrac{{25}}{{\left( {200 - 25} \right)}} = \dfrac{{25}}{{175}} = \dfrac{1}{7}$
So, this is the required ratio of the two parts of the cone.
So, this is the required answer.

Note – In such types of questions always remember the formula of cone which is stated above then first of all using the property of similar triangles calculate the value of base radius of smaller cone as above and the cone is cut from the midpoint so the height of the smaller cone is equal to the height of lower part of the bigger solid cone which is equal to half of the height of bigger solid cone, then take the ratio of volume of smaller cone to the volume of lower part of the big solid cone as above and simplify which is the required ratio in the volumes of two parts of the cone.