Question

A sector subtends an angle of measure 120° at the centre of a circle having radius of 21 cm. The area of the sector is (in $cm^2$)
A. 462
B. 460
C. 465
D. 470

Answer 1

Hint: The sector is basically a portion of a circle which is enclosed by two radii and an arc. A sector divides the circle into two regions, namely major and minor sectors. The smaller area is known as the minor sector, whereas the region having a greater area is known as the major sector.
The area of a sector of the circle is calculated by using the formula:
Area =$\pi {r^2} \times \left( {\dfrac{\theta }{{360^\circ }}} \right)$, where ‘θ’ is the angle subtended at the centre.

Complete step by step solution:
Here, according to the question
Radius of the sector = 21 cm
Angle subtended by the arc at centre= θ = 120°

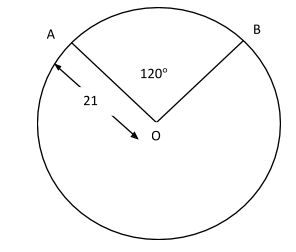
Now, we calculate the area of sector OAB
Area of the sector = $\pi {r^2}\dfrac{\theta }{{360}}$
$\begin{gathered}
   = \dfrac{{22}}{7} \times 21 \times 21 \times \dfrac{{120}}{{360}} \\
   = \dfrac{{22 \times 21 \times 21}}{{7 \times 3}} \\
   = 462c{m^2} \\
\end{gathered} $
Therefore, the area of the sector is 462 $cm^2$

Note: If the length of the arc of the sector is given instead of the angle of the sector, then we will use the different method to calculate the area of the sector. Let the length of the arc be ‘l’. For the radius of a circle equal to r units, an arc of length r units will subtend 1 radian at the centre. Hence, it can be concluded that an arc of length ‘l’ will subtend$\dfrac{l}{r}$, the angle at the centre. So, if l is the length of the arc, r is the radius of the circle and θ is the angle subtended at the centre, then;
$\theta = \dfrac{l}{r}$, where θ is in radian. Therefore, the area of sector = $A = \dfrac{{\left( {lr} \right)}}{2}$