Question

A room is 7.5 m long, 5.5 m broad and 5 m high. What will be the expenditure in covering the walls by paper 40 cm broad at the rate of 80 paise per metre?

Answer 1

Hint: The room is in the form of a cuboid and we have to cover the walls of the room. The room has 4 walls so find the surface area of 4 walls which is equal to $2h\left( l+b \right)$. In this formula, l, b and h are the length, breadth and height of the room. After that we have given the breadth of the paper but we require length of the paper which we will calculate by dividing area by breadth then we have given the cost for 1 m so multiply the length in metres by 0.80 Rs to get the cost of the paper.

Complete step by step answer:
We have given a room with length, breadth and height as 7.5 m, 5.5 m and 5 m respectively. The room is given in the form of a cuboid.
In the below figure, we have shown the room with length, breadth and height as 7.5 m, 5.5 m and 5 m respectively.

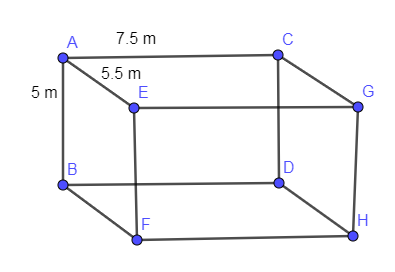
Now, we have to cover the walls of this room with paper. The walls that need to be covered are (ACDB, EGHF, AEFB and CGHD). We are going to find the surface area of these four walls.
Let us assume that length, breadth and height of the room is l, b and h respectively then surface area of the four walls that we have mentioned above is:
$2h\left( l+b \right)$
Substituting the value of l, b and h as 7.5 m, 5.5 m and 5 m respectively in the above formula we get,
$\begin{align}
  & 2\left( 5 \right)\left( 7.5+5.5 \right) \\
 & =10\left( 13.0 \right) \\
 & =130{{m}^{2}} \\
\end{align}$
From the above calculations, we have found the surface area of four walls as $130{{m}^{2}}$.
Now, we have given the paper of 40 cm broad or (breadth) and we require the length of the paper. The paper is in the form of rectangle so we know that,
Area of rectangle $=\left( length \right)\left( breadth \right)$…………. Eq. (1)
The total area of four walls we know so equating that area with the multiplication of length and breadth we get,
$130=\left( length \right)\left( 40cm \right)$………. Eq. (2)
Now, area is given in ${{m}^{2}}$ and breadth of the paper is given in cm so we have to convert breadth of the paper into m by dividing 40 by 100 we get,
$\begin{align}
  & \dfrac{40}{100}m \\
 & =0.40m \\
\end{align}$
Substituting this value in eq. (1) in place of 40 cm we get,
$130=\left( length \right)\left( 0.40m \right)$
Dividing 0.40 on both the sides of the above equation we get,
$\begin{align}
  & \dfrac{130}{0.4}=length \\
 & \Rightarrow 325m=length \\
\end{align}$
The cost of 1 m paper is given as 80 paise.
Converting 80 paise into rupees by dividing 80 by 100 we get,
$\begin{align}
  & \dfrac{80}{100}Rs \\
 & 0.80Rs \\
\end{align}$
Now, the cost of 1 m paper is Rs 0.80 so the cost of 325 m is calculated by multiplying 325 by 0.80.
Multiplying 325 by 0.80 we get,
$\begin{align}
  & 325\left( 0.8 \right) \\
 & =Rs 260 \\
\end{align}$

Hence, the cost of covering the four walls by paper is Rs 260.

Note: The blunder that could happen in this problem is in writing the curved surface. Generally, in the rush of completing the exam students tend to write the total surface area of the cuboid which we are shown below:
$2\left( lb+bh+hl \right)$
But the question is saying, we just have to cover the walls of the room and exclude the ceiling and floor of the room so be careful while writing the surface areas of the walls of the room which is $2h\left( l+b \right)$.