Question

A reservoir is in the shape of a frustum of a right circular cone; it is \[8m\] across at the top and \[4m\] across at the bottom. If it is \[6m\] deep its capacity is.

Answer 1

Hint: Here we use the concept of volume of frustum. We need to find the capacity of the reservoir which is in the shape of frustum.
$\text{V}olume\text{ }of\text{ }frustrum\text{ }of\text{ }cone=\dfrac{1}{3}\pi h({{R}^{2}}+{{r}^{2}}+Rr)$

Complete step by step answer:
Frustum is the slice part of a cone.

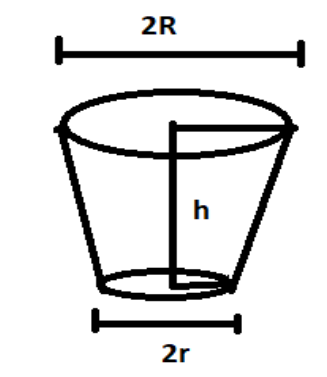
 Let $R$ be the radius of Upper frustum of a right circular cone.
$r$ be the radius of Lower frustum of a right circular cone.
$h$ be the depth or height of frustum.
\[Lower\text{ }radius\text{ }of\text{ }frustum\text{ }of\text{ }cone\text{ }\left( \text{r} \right)\text{=}\dfrac{Lower\text{ }diameter\text{ }of\text{ }frustum\text{ }}{2}=\dfrac{4}{2}=2m\]
$Upper\text{ }radius\text{ }of\text{ }frustum\text{ }of\text{ }cone\text{ (R)=}\dfrac{upper\text{ }diameter\text{ }of\text{ }frustum}{2}=\dfrac{8}{2}=4m$
According to question,
Capacity of the reservoir becomes the volume of the frustum.
$\text{V}olume\text{ }of\text{ reservoir}=\dfrac{1}{3}\pi h({{R}^{2}}+{{r}^{2}}+Rr)$
$\begin{align}
  & =\dfrac{1}{3}\times \pi \times 6({{4}^{2}}+{{2}^{2}}+4\times 2) \\
 & =2\pi \times (16+4+8) \\
 & =2\pi \times 28 \\
 & =56\pi \\
 & =56\times \dfrac{22}{7} \\
 & =8\times 22 \\
 & =176 \\
\end{align}$

Therefore, Capacity of reservoir in the shape of a frustum of a right circular cone frustum is $176\,{{m}^{3}}$.

Note: In such types of questions which involves the concept of 3D figures having knowledge about the terms related to the figures is needed. Follow up accordingly by assigning the data in the formula to get the required value.