Question

A regular hexagon of maximum possible area is cut off from an equilateral triangle. The ratio of area of triangle to the area of hexagon will be
A. $\sqrt {\dfrac{3}{2}} $
B. $\dfrac{{\sqrt 6 }}{2}$
C. $\dfrac{3}{{\sqrt 2 }}$
D. $\dfrac{3}{2}$

Answer 1

Hint: Regular hexagons are six sided figures. In a regular hexagon, all sides are of the same length and all interior angles have the same measure. One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Each angle in the triangle is 60°, each triangle has three equal side lengths and three equal angles. If we find the area of one of the triangles, then we can multiply it by six in order to calculate the area of the hexagon.
Area of equilateral triangle =$\dfrac{{\sqrt 3 }}{4}{s^2}$, where‘s’ is the side of the triangle

Complete step by step solution: Let 3a be the sides of equilateral triangle PQR

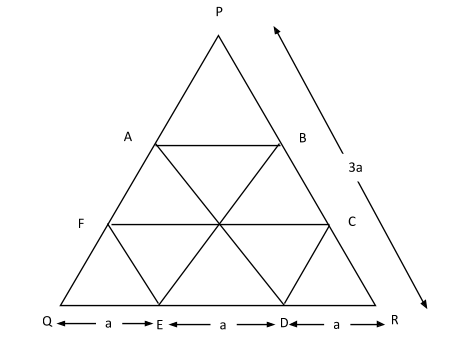
The area of equilateral triangle =$arPQR = \dfrac{{\sqrt 3 }}{4}{a^2}$
$\begin{gathered}
  arPQR = \dfrac{{\sqrt 3 }}{4} \times 3a \times 3a \\
  arPQR = \dfrac{{9\sqrt 3 }}{4}{a^2} \\
\end{gathered} $
We know that a regular hexagon is formed by joining 6 equilateral triangles. Hence side of regular hexagon inscribed from an equilateral $\Delta PQR$ is $\dfrac{{3a}}{3} = a$
Therefore, Area of hexagon $ABCDEF = 6 \times \dfrac{{\sqrt 3 }}{4} \times {a^2} = \dfrac{{6\sqrt 3 }}{4}{a^2}$
The ratio of area of equilateral triangle to the area of hexagon $ = \dfrac{{ar\Delta PQR}}{{arABCDEF}}$
$\begin{gathered}
  \dfrac{{ar\Delta PQR}}{{arABCDEF}} = \dfrac{{\dfrac{{9\sqrt 3 }}{4}{a^2}}}{{\dfrac{{6\sqrt 3 }}{4}{a^2}}} = \dfrac{9}{6} \\
  \dfrac{{ar\Delta PQR}}{{arABCDEF}} = \dfrac{3}{2} \\
\end{gathered} $
Hence, the ratio of area of equilateral triangle to the area of hexagon is $\dfrac{3}{2}$
∴Option (D) is correct.

Note: If we know the side length, we can find the area of hexagon directly by the formula. Therefore, the formula for finding the area of a hexagon is derived by using the formula of equilateral triangle, hence the area of hexagon, where‘s’ is the length of a side of regular hexagon is:
Area of hexagon = $\dfrac{{3\sqrt 3 {s^2}}}{2}$