Question

A rectangular field is 20 m long and 14 m wide. There is a path of equal width around it, having an area of 111 sq.m. Find the width of the path?

Answer 1

Hint: We are given the dimensions of the rectangular field and assuming the width of the path around it to be x we get the dimensions of the new rectangle to be $20 + 2x$m and $14 + 2x$m and it's clear that the area of the path is equal to the difference of the areas of the rectangles hence we find the area of the rectangles using the formula $Area = l\times b$ and further equating the area of the path with difference we get the value of x.

Complete step by step solution:
We are given the length and width of a rectangular field to be 20 m and 14 m

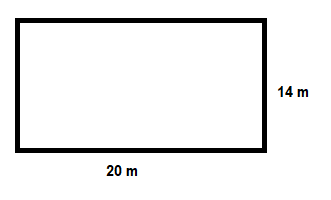
Now we are given that there is a path around the field with equal width
Let the width of the path be x
Now from the diagram we can see that now the length and breadth of the new rectangle is $20 + 2x$m and $14 + 2x$m respectively.

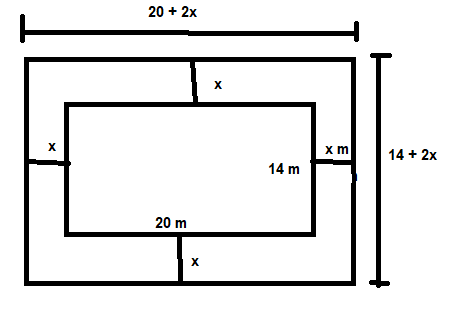
We are given the area of the path that is the area of the shaded region is 111 sq.m.

This area is obtained by subtracting the area of the small rectangle from the area of the big rectangle
We know that the length and breadth of the small rectangle is 20 m and 4 m respectively.
Hence the area of the small rectangle is given by
$
   \Rightarrow Area = l\times b \\
   \Rightarrow Area = 20\times 14 \\
   \Rightarrow Area = 280{m^2} \\
 $
We know that the length and breadth of the big rectangle is $20 + 2x$m and $14 + 2x$m respectively
Hence the area of the big rectangle is given by
$
   \Rightarrow Area = l\times b \\
   \Rightarrow Area = \left( {20 + 2x} \right)\left( {14 + 2x} \right) \\
   \Rightarrow Area = 280 + 40x + 28x + 4{x^2} \\
   \Rightarrow Area = \left( {280 + 68x + 4{x^2}} \right){m^2} \\
 $
Now since
Area of the path = the difference between the areas of the rectangles
$
   \Rightarrow 111 = 280 + 68x + 4{x^2} - 280 \\
   \Rightarrow 111 = 68x + 4{x^2} \\
   \Rightarrow 4{x^2} + 68x - 111 = 0 \\
   \Rightarrow 4{x^2} - 6x + 74x - 111 = 0 \\
   \Rightarrow 2x\left( {2x - 3} \right) + 37\left( {2x - 3} \right) = 0 \\
   \Rightarrow \left( {2x - 3} \right)\left( {2x + 37} \right) = 0 \\
   \Rightarrow x = \dfrac{3}{2},\dfrac{{ - 37}}{2} \\
 $
Since the width cannot be negative we take the value of x to be $\dfrac{3}{2}$m

Therefore the width of the path is $\dfrac{3}{2}$m.

Note :
Many students tend to write the dimension of the new triangle to be 20 + x and 14 + x
But since the width is added on both sides we need to add 2x on both sides.