Question

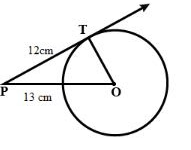
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle

Answer 1

Hint: Use the information that tangent to a circle is perpendicular to the radius through the point of contact.

We know that, tangent to a circle is perpendicular to the radius through the point of contact. So, $\angle OTP = {90^ \circ }$. In right angle triangle OTP, we have

$
  O{P^2} = O{T^2} + P{T^2} \\
   \Rightarrow {13^2} = O{T^2} + {12^2} \\
   \Rightarrow O{T^2} = {13^2} - {12^2} \\
   \Rightarrow O{T^2} = 169 - 144 \\
   \Rightarrow O{T^2} = 25 \\
   \Rightarrow OT = 5 \\
$
Hence the radius of the circle is 5 cm.
Note: Using the correct theorem is the key to solve this problem. After that Pythagoras theorem will give the required result.