Question

A plane is flying horizontally at a height of 1km from the ground. Angle of elevation of the plane at a certain instant is \[\text{6}{{\text{0}}^{0}}\] . After 20s, the angle of elevation is found \[\text{3}{{\text{0}}^{0}}\] . The speed of the plane is:

Answer 1

Hint: Refer to the figure.Consider the distance AB as x and AC as y. Apply \[\tan {{60}^{0}}\] in the \[\Delta PAB\] and \[\tan {{30}^{0}}\] in the \[\Delta QAC\] . We know the formula of speed, \[speed=\dfrac{\text{distance}}{\text{time}}\]. Here, distance is AC-AB and time is 20s. Now, it will be solved further.

Complete step by step answer:
Analyze both the conditions using a diagram. The height of the plane at which it is flying remains constant. The diagram is shown below.

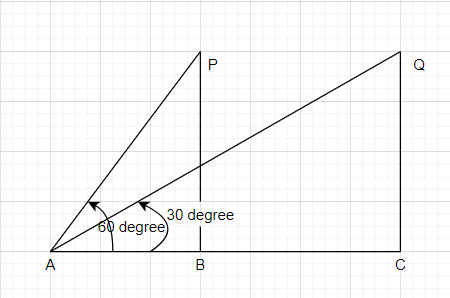
In triangle PAB apply, \[\tan {{60}^{0}}\] and find the distance AB. Similarly, apply \[\tan {{30}^{0}}\] in the triangle QAC and find the distance AC. Calculate the distance, AC-AB. Then using the formula \[speed=\dfrac{\text{distance}}{\text{time}}\] , speed can be calculated.
Assume the distance AB=x and AC=y
The height at which the plane is flying remains the same.
PA=QC=1km.
In the triangle, PAB we have
\[\begin{align}
  & \tan {{60}^{0}}=\dfrac{1}{x} \\
 & \Rightarrow \sqrt{3}=\dfrac{1}{x} \\
 & \Rightarrow x=\dfrac{1}{\sqrt{3}} \\
\end{align}\]
Similarly, in triangle QAC we have,
\[\begin{align}
  & \tan {{30}^{0}}=\dfrac{1}{y} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{1}{y} \\
 & \Rightarrow y=\sqrt{3} \\
\end{align}\]
Distance covered in 20sec=(AC-AB)km
\[y-x=\sqrt{3}-\dfrac{1}{\sqrt{3}}=\dfrac{3-1}{\sqrt{3}}=\dfrac{2}{\sqrt{3}}km=\dfrac{2000}{\sqrt{3}}m\].
We know, \[speed=\dfrac{\text{distance}}{\text{time}}=\dfrac{\dfrac{2000}{\sqrt{3}}}{20}=\dfrac{100}{\sqrt{3}}m/s\].

Hence, the speed of the plane is \[\dfrac{100}{\sqrt{3}}\,\,m/s\] .

Note: In this type of question, pictorial representation is important and the formula of speed is to be remembered. That is, \[speed=\dfrac{\text{distance}}{\text{time}}\]. Here, one can take the distance AC(as shown in diagram) as distance in the given formula, which is wrong. The correct distance should be AC-AB.