Question

A pit $ 7{\text{ m}} $ long and $ 3.5{\text{ m}} $ wide is dug to a certain depth. If the volume of earth taken out of it is $ 98{\text{ }}{{\text{m}}^3} $ , what is the depth of the pit?

Answer 1

Hint: The volume of parallelepiped is equal to the product of length, breadth and height. The volume of earth taken out is equal to the volume parallelepiped from this equality the depth can be found.

Complete step-by-step answer:
 A pit is $ 7{\text{ m}} $ long and $ 3.5{\text{ m}} $ wide.
The volume of earth taken out of the pit is $ 98{\text{ }}{{\text{m}}^3} $ .

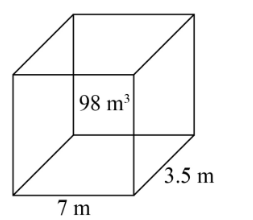
A pit is of the rectangular parallelepiped form. A parallelepiped is a bounded figure with $ 6 $ parallelograms where opposite sides are similar and parallel.
The volume of the parallelepiped is equal to the product of length, breadth and height. In our problem the parallelepiped is pit with length $ 5{\text{ m}} $ and breadth of $ 3.5{\text{ m}} $ .
Let us assume the height of the pit to be $ d{\text{ m}} $ .
On using the formula for volume of parallelepiped, we get,
 $
\Rightarrow {\text{ volume of pit }} = 7 \times 3.5 \times d\\
 = 24.5d{\text{ }}{{\text{m}}^3}
 $ …….(1)
It is given that volume of earth taken out is equal to the volume of pit, then we can say that,
 $ {\text{volume of pit}} = 98\;{{\text{m}}^3} $ ………(2)
Since, (1) and (2) represent the same quantity we equate the both equations then we obtain,
 $
\Rightarrow 24.5d = 98\\
\Rightarrow d = \dfrac{{98}}{{24.5}}{\text{ m}}\\
\Rightarrow d = 4\;{\text{m}}
 $
Hence, the depth of the pit is $ 4{\text{ m}} $ .
So, the correct answer is “ $ 4{\text{ m}} $ ”.

Note: There is also an alternate method to solve this problem. Since, we know $ 98 $ is equal to length, breadth and height. Everything is known except height. From the equation we directly get the depth value.