Question

A person observed the angle of elevation of the top of a tower as \[{{30}^{\circ }}\]. He walked 50 m towards the foot of the angle of elevation of the top of the tower as \[{{60}^{\circ }}\]. Find the height of the tower.

Answer 1

Hint: consider the height of the tower as AB and draw the angle of elevations at two different points and apply \[\tan \theta \]to the two right angled triangles and we will get two equations and then we have to compute the height of the tower.

Complete step-by-step answer:

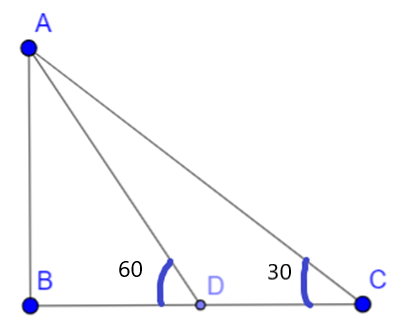
Given, the angle of elevation of top of tower is \[{{30}^{\circ }}\]

Then he walked 50m towards the foot of angle of elevation of top of tower and now the angle of elevation is \[{{60}^{\circ }}\]

Let the Height of the Tower be AB

In the right angled triangle ABC

\[\tan \theta =\dfrac{AB}{BC}\]. . . . . . . . . . . . . . . . . . . (1)

\[\tan {{30}^{\circ }}=\dfrac{h}{x+50}\]

\[\dfrac{1}{\sqrt{3}}=\dfrac{h}{x+50}\]

\[\sqrt{3}h=x+50\]. . . . . . . . . . . . . . . . . (2)

In the right angled triangle ABD

\[\tan \theta =\dfrac{AB}{BD}\]. . . . . . . . . . . . . . . . . . . . . . (5)

\[\tan {{60}^{\circ }}=\dfrac{h}{x}\]

\[\sqrt{3}=\dfrac{h}{x}\]

\[h=\sqrt{3}x\]

\[x=\dfrac{h}{\sqrt{3}}\]. . . . . . . . . . . . . . . . . . . . . . . . (4)

Substitute \[x=\dfrac{h}{\sqrt{3}}\]in equation (2)

\[\sqrt{3}h=\dfrac{h}{\sqrt{3}}+50\]

\[3h=h+50\sqrt{3}\]

\[2h=50\sqrt{3}\]

\[h=25\sqrt{3}\]m

So, the height of the tower obtained is AB=\[h=25\sqrt{3}=43.3m\]

Note: the angle of elevation is the angle between the horizontal line from the observer and the line of sight to an object that is above the horizontal line. As the person moves from one point to another angle of elevation varies. If we move closer to object the angle of elevation increases and vice versa