Question

A peacock is sitting on the top of a pillar, which is 9 m high. From a point 27 m away from the bottom of the pillar a snake is coming to its hole at the base of the pillar. Seeing the snake the peacock pounces on it. If their speeds are equal, at what distance from the whole snake is it caught?

Answer 1

Hint: Here, we will use the concepts of speed and distance as well as the Pythagorean Theorem i.e.., sum of squares of two adjacent sides of a triangle is equal to the square of the hypotenuse in a right angle triangle.
Given,
A peacock is sitting on the top of a pillar, which is 9 m high, so let us consider ‘A’ is the position of peacock and ‘AB’ be the pillar which is 9 m high. Now, it is also given that from a point 27 m away from the bottom of the pillar a snake is coming to its hole at the base of the pillar. Therefore, let ‘C’ be the position of the snake at the bottom of the pillar. Therefore, the representation is as follows:

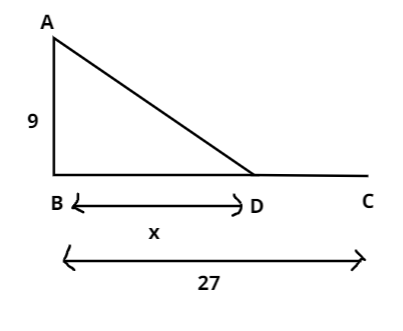
Let Peacock catch the snake at a distance of ‘x’ m from the bottom of the pillar. So, $AB = 9, BD = x, BC = 27$. Hence the value of ‘DC’ can be written as
$
   \Rightarrow DC = BC - BD \\
   \Rightarrow DC = 27 - x \\
 $
Now, Using the Pythagorean Theorem, let us find the distance covered by peacock i.e.., AD
$
   \Rightarrow A{D^2} = B{C^2} + A{B^2} \\
   \Rightarrow A{D^2} = {x^2} + {9^2} \\
   \Rightarrow A{D^2} = {x^2} + 81 \\
   \Rightarrow AD = \sqrt {{x^2} + 81} \\
$
It is mentioned that the speed of peacock and snake are equal. Therefore, distance covered by the peacock and distance covered by the snake will be equal i.e..,
${\text{Distance covered by peacock(AD) = Distance covered by snake (DC)}}$
$
   \Rightarrow AD = DC \\
   \Rightarrow \sqrt {{x^2} + 81} = 27 - x \\
$
Squaring on the both sides, we get
$
   \Rightarrow {(\sqrt {{x^2} + 81} )^2} = {(27 - x)^2} \\
   \Rightarrow {x^2} + 81 = 729 + {x^2} - 54x \\
   \Rightarrow 54x = 729 - 81 \\
   \Rightarrow 54x = 648 \\
   \Rightarrow x = \dfrac{{648}}{{54}} = 12 \\
$
Hence, the snake got caught at a distance of 12m.
Note: As, the speeds of peacock and snake are equal, we have considered distance covered by peacock and snake are equal.