Question

A metal pipe has an external diameter of 4cm and internal diameter of 3cm and is 20cm long, then the volume of the metal rod used is: -
(a) \[22c{{m}^{3}}\]
(b) \[110c{{m}^{3}}\]
(c) \[220c{{m}^{3}}\]
(d) \[440c{{m}^{3}}\]

Answer 1

Hint: Consider the metal pipe in the form of a cylinder and assume the external radius as R and internal radius as r. Assume ‘h’ as the length of this pipe. Now, calculate the values of internal and external radius by using the relation: - radius = (diameter / 2). Now, find the volume of the metal rod used by using the formula of volume of a cylindrical shell given as: - Volume = \[\pi \left( {{R}^{2}}-{{r}^{2}} \right)h\]. Substitute the values to get the answer. Use \[\pi =\dfrac{22}{7}\].

Complete step by step solution:
Here, we have been provided with a metal pipe with an external diameter of 4cm and internal diameter of 3cm. The length of the pipe is given as 20cm. We are asked to calculate the volume of the metal used.
Now, we know that the given pipe will be in the form of a cylinder with some thickness, called a cylindrical shell. So, let us draw a rough diagram of the above situation.

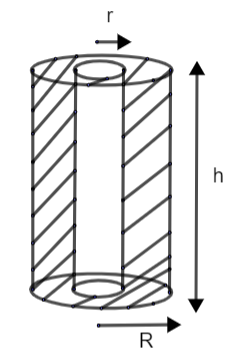
In the above figure, we have considered a cylindrical shell with internal radius as ‘r’ and external radius as ‘R’. We have assumed the height of this shell as ‘h’. So, considering it as the metal pipe let us find the values of R and r using the relation: - radius = (diameter / 2). Therefore, we have,
\[\Rightarrow \] R = External radius = (External diameter / 2)
\[\Rightarrow R=\dfrac{4}{2}\] cm
\[\Rightarrow \] r = Internal radius = (Internal diameter / 2)
\[\Rightarrow r=\dfrac{3}{2}\] cm
Also, we have, h = height = 20cm.
Now, the volume of metal used for the construction will be the volume of metal present in between the external and internal cylinder. It is denoted by the shaded part in the above figure. So, we have,
\[\Rightarrow \] Volume of metal used = \[\pi {{R}^{2}}h-\pi {{r}^{2}}h\]
This is because the volume of a cylinder is given as: - Volume = \[\pi {{r}^{2}}h\].
So, we have,
\[\Rightarrow \] Volume of metal used = \[\pi h\left( {{R}^{2}}-{{r}^{2}} \right)\]
Using the algebraic identity: - \[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\], we get,
\[\Rightarrow \] Volume of metal used = \[\pi h\left( R+r \right)\left( R-r \right)\]
Substituting the values of h, R and r, we get,
\[\Rightarrow \] Volume = \[\pi \times 20\times \left( \dfrac{4}{2}+\dfrac{3}{2} \right)\left( \dfrac{4}{2}-\dfrac{3}{2} \right)\]
Using the value \[\pi =\dfrac{22}{7}\], we get,
\[\Rightarrow \] Volume = \[\dfrac{22}{7}\times 20\times \dfrac{7}{2}\times \dfrac{1}{2}\]
\[\Rightarrow \] Volume = \[110c{{m}^{3}}\]
Hence, option (b) is the correct answer.

Note: One must remember the formula of volume of a cylindrical shell, spherical shell, hemispherical shell and other basic 3 – D shapes. Do not forget to draw a rough diagram of the given situation as it will help us to visualize the situation in a better way. You may see that here we have used the value \[\pi =\dfrac{22}{7}\], this was done to make the calculation easy. You may use \[\pi =3.14\] as it will not affect the answer much, you will get some value near about \[110c{{m}^{3}}\].