A man walking due north, observes that the elevation of a balloon, which is due east of him and is sailing towards the north-west is then ${60^\circ }$, after he has walked 400 yards the balloon is vertically over his head. Find its height supposing it has always remained the same.
Verified147.3k+ views
Hint: We are using trigonometric equations, first horizontally and second in case of vertical equations of the balloon. First determine the distance covered by balloon and then the vertical elevation. Value obtained from the first part should be used while calculating for the ultimate answer.
Complete step-by-step answer:
Let assume at first place the man standing at point A and then he went to point C. The balloon is finally at point B, just vertically at his head. Man and balloon were moving during the same duration.
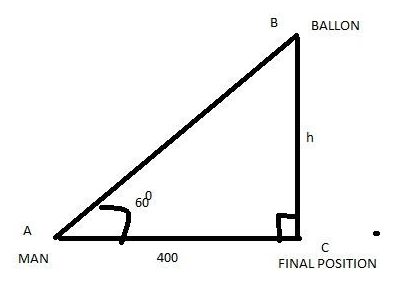
Height of the balloon is h meter as our assumption. Angle of elevation of the balloon initially was ${60^0}$. So, in the diagram $\vartriangle ABC$, we have
$\angle BAC = {60^0}$
AC = 400 yards
BC= h yards
So, from the trigonometry, we know that,
$
\tan A = \dfrac{{perpendicular}}{{base}} \\
\Rightarrow \tan A = \dfrac{{BC}}{{AC}} \\
$
Thus, substitute the values, we get
$
\tan {60^0} = \dfrac{h}{{400}} \\
\Rightarrow \sqrt 3 = \dfrac{h}{{400}} \\
\Rightarrow h = 400\sqrt 3 \\
$
Since $\sqrt 3 = 1.732$
So, height will be,
$
h = 400 \times 1.732 \\
\Rightarrow h = 692.8 yards \\
$
$\therefore $ The height of the balloon is 692.8 yards from the ground.
Additional Information: Trigonometry is a very interesting and useful branch of mathematics. It has several ratios, identities, formulas and theories. Many problems of real-life as well as of science are solvable through trigonometry. The above problem is one such example. It is an example of Height and Distances problems.
Note: In this type of question visualization and knowledge of trigonometric is very important. The numerical values of different trigonometric functions for different angles should be taken carefully & while equating the relations to get the unknown, calculations should be done attentively so that there would be no chance of technical error.
Complete step-by-step answer:
Let assume at first place the man standing at point A and then he went to point C. The balloon is finally at point B, just vertically at his head. Man and balloon were moving during the same duration.
Height of the balloon is h meter as our assumption. Angle of elevation of the balloon initially was ${60^0}$. So, in the diagram $\vartriangle ABC$, we have
$\angle BAC = {60^0}$
AC = 400 yards
BC= h yards
So, from the trigonometry, we know that,
$
\tan A = \dfrac{{perpendicular}}{{base}} \\
\Rightarrow \tan A = \dfrac{{BC}}{{AC}} \\
$
Thus, substitute the values, we get
$
\tan {60^0} = \dfrac{h}{{400}} \\
\Rightarrow \sqrt 3 = \dfrac{h}{{400}} \\
\Rightarrow h = 400\sqrt 3 \\
$
Since $\sqrt 3 = 1.732$
So, height will be,
$
h = 400 \times 1.732 \\
\Rightarrow h = 692.8 yards \\
$
$\therefore $ The height of the balloon is 692.8 yards from the ground.
Additional Information: Trigonometry is a very interesting and useful branch of mathematics. It has several ratios, identities, formulas and theories. Many problems of real-life as well as of science are solvable through trigonometry. The above problem is one such example. It is an example of Height and Distances problems.
Note: In this type of question visualization and knowledge of trigonometric is very important. The numerical values of different trigonometric functions for different angles should be taken carefully & while equating the relations to get the unknown, calculations should be done attentively so that there would be no chance of technical error.