Questions & Answers
Question
Answers
Related Questions
A man on the top of the rock observed a boat coming towards the rock with a uniform speed. It takes 15 minutes for the angle of depression to change from ${{60}^{\circ }}$ to ${{30}^{\circ }}$then what time will the boat take to reach the shore?
(a) 5 minutes
(b) 10 minutes
(c) $7\dfrac{1}{2}$ minutes
(d) $2\dfrac{1}{2}$ minutes
Answer
![Verified]()
Verified
Verified
Hint: First, before proceeding for this, we must know the following situation to be shown in the diagram where h is the height of the rock. Then, from the figure it is clear that we can use the right angles triangle properties so that we can get the distance travelled by boat. Then, using the same property of the trigonometry for another triangle ABC. Then, we know the formula for the speed, distance and time where v is speed, t is time and d is distance as $v=\dfrac{d}{t}$, we get the final result.
Complete step-by-step answer:
In this question, we are supposed to find the time the boat will take to reach the shore.
So, before proceeding for this, we must know the following situation to be shown in the diagram where h is the height of the rock.
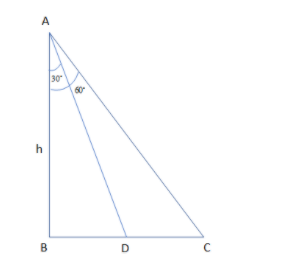
Now, from the figure it is clear that we can use the right angles triangle properties so that we can get the distance travelled by boat as:
$\tan {{30}^{\circ }}=\dfrac{h}{BC}$
So, by solving the above expression, we get:
$\begin{align}
& \dfrac{1}{\sqrt{3}}=\dfrac{h}{BC} \\
& \Rightarrow BC=h\sqrt{3} \\
\end{align}$
Now, by using the same property of the trigonometry for another triangle ABD is as:
$\tan {{60}^{\circ }}=\dfrac{h}{BD}$
So, by solving the above expression, we get:
$\begin{align}
& \sqrt{3}=\dfrac{h}{BD} \\
& \Rightarrow BD=\dfrac{h}{\sqrt{3}} \\
\end{align}$
Now, the distance travelled by boat in 15 minutes is given by the subtraction of the above two calculations as:
$h\sqrt{3}-\dfrac{h}{\sqrt{3}}$
Now, we know the formula for the speed, distance and time where v is speed, t is time and d is distance as:
$v=\dfrac{d}{t}$
So, by substituting the values of distance from above calculation and value of times as 15 minutes:
$\begin{align}
& v=\dfrac{h\sqrt{3}-\dfrac{h}{\sqrt{3}}}{15} \\
& \Rightarrow v=\dfrac{3h-h}{15\times \sqrt{3}} \\
& \Rightarrow v=\dfrac{2h}{15\sqrt{3}} \\
\end{align}$
So, to reach the shore, the boat needs to travel a distance of $\dfrac{h}{\sqrt{3}}$ in time t.
Then, it gives the value of time t as:
$\begin{align}
& t=\dfrac{\dfrac{h}{\sqrt{3}}}{\dfrac{2h}{15\sqrt{3}}} \\
& \Rightarrow t=\dfrac{h}{\sqrt{3}}\times \dfrac{15\sqrt{3}}{2h} \\
& \Rightarrow t=\dfrac{15}{2} \\
& \Rightarrow t=7\dfrac{1}{2} \\
\end{align}$
So, the time required by the boat to reach the shore is $7\dfrac{1}{2}$ minutes.
Hence, option (c) is correct.
Note: Now, to solve these types of the questions we need to know some of the basic trigonometric calculations of the angles from the right angles triangle. So, the basic calculation formulas are as:
$\tan \theta =\dfrac{P}{B}$ where P is perpendicular and B is base.
$\sin \theta =\dfrac{P}{H}$ where P is perpendicular and H is hypotenuse.
$\cos \theta =\dfrac{B}{H}$ where B is base and H is hypotenuse.
Complete step-by-step answer:
In this question, we are supposed to find the time the boat will take to reach the shore.
So, before proceeding for this, we must know the following situation to be shown in the diagram where h is the height of the rock.
Now, from the figure it is clear that we can use the right angles triangle properties so that we can get the distance travelled by boat as:
$\tan {{30}^{\circ }}=\dfrac{h}{BC}$
So, by solving the above expression, we get:
$\begin{align}
& \dfrac{1}{\sqrt{3}}=\dfrac{h}{BC} \\
& \Rightarrow BC=h\sqrt{3} \\
\end{align}$
Now, by using the same property of the trigonometry for another triangle ABD is as:
$\tan {{60}^{\circ }}=\dfrac{h}{BD}$
So, by solving the above expression, we get:
$\begin{align}
& \sqrt{3}=\dfrac{h}{BD} \\
& \Rightarrow BD=\dfrac{h}{\sqrt{3}} \\
\end{align}$
Now, the distance travelled by boat in 15 minutes is given by the subtraction of the above two calculations as:
$h\sqrt{3}-\dfrac{h}{\sqrt{3}}$
Now, we know the formula for the speed, distance and time where v is speed, t is time and d is distance as:
$v=\dfrac{d}{t}$
So, by substituting the values of distance from above calculation and value of times as 15 minutes:
$\begin{align}
& v=\dfrac{h\sqrt{3}-\dfrac{h}{\sqrt{3}}}{15} \\
& \Rightarrow v=\dfrac{3h-h}{15\times \sqrt{3}} \\
& \Rightarrow v=\dfrac{2h}{15\sqrt{3}} \\
\end{align}$
So, to reach the shore, the boat needs to travel a distance of $\dfrac{h}{\sqrt{3}}$ in time t.
Then, it gives the value of time t as:
$\begin{align}
& t=\dfrac{\dfrac{h}{\sqrt{3}}}{\dfrac{2h}{15\sqrt{3}}} \\
& \Rightarrow t=\dfrac{h}{\sqrt{3}}\times \dfrac{15\sqrt{3}}{2h} \\
& \Rightarrow t=\dfrac{15}{2} \\
& \Rightarrow t=7\dfrac{1}{2} \\
\end{align}$
So, the time required by the boat to reach the shore is $7\dfrac{1}{2}$ minutes.
Hence, option (c) is correct.
Note: Now, to solve these types of the questions we need to know some of the basic trigonometric calculations of the angles from the right angles triangle. So, the basic calculation formulas are as:
$\tan \theta =\dfrac{P}{B}$ where P is perpendicular and B is base.
$\sin \theta =\dfrac{P}{H}$ where P is perpendicular and H is hypotenuse.
$\cos \theta =\dfrac{B}{H}$ where B is base and H is hypotenuse.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
