Question

A lotus flower is blooming in a lake. The flower is $\dfrac{1}{2}$ meter above the surface of the lake. When western winds blow, the flower drops at a distance of $2m$ from the base. Find the depth of the lake.

Answer 1

Hint- Try to find out all the dimensions by the help of a figure and the statements given in the question. Look for some geometrical way of solving the problem, by finding some geometrical figures and formulas.

“Complete step-by-step answer:”
Given that: Lotus is blooming in the lake as shown in the figure. The flower is $\dfrac{1}{2}$ meter above the surface of the lake.

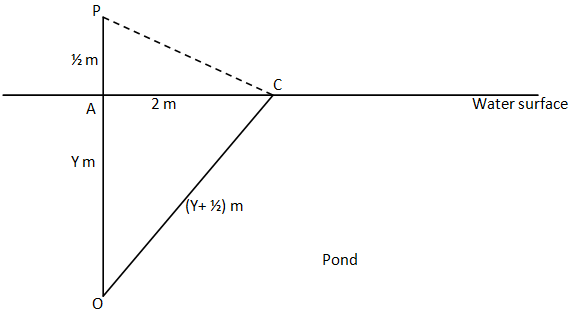
Let O is the lowest point of the root of lotus or the base of the lake. AP is the part above the surface of water and OA is the part of the lotus below the water at normal position.
When the western winds blow, the flower drops at a distance of $2m$ from the base point. And the flower is displaced from OP to OC.
Since the length of the stem of the flower will be same so
$
   \Rightarrow OC = OA + OP \\
   \Rightarrow OC = \left( {Y + \dfrac{1}{2}} \right)m \\
 $
AC is the distance between the displaced points which is $2m$.
So the depth of the lake $ = Ym$
Taking water to be horizontal and the stem to be perfectly straight. We have $\Delta OAC$ is a right angled triangle.
So using Pythagoras theorem we get:
$
   \Rightarrow {\left( {OC} \right)^2} = {\left( {OA} \right)^2} + {\left( {AC} \right)^2} \\
   \Rightarrow {\left( {Y + \dfrac{1}{2}} \right)^2} = {\left( Y \right)^2} + {\left( 2 \right)^2} \\
   \Rightarrow {Y^2} + {\left( {\dfrac{1}{2}} \right)^2} + 2 \times Y \times \dfrac{1}{2} = {Y^2} + 4\left[ {\because {{\left( {a + b} \right)}^2} = {a^2} + {b^2} + 2 \times a \times b} \right] \\
   \Rightarrow {Y^2} + \dfrac{1}{4} + Y = {Y^2} + 4 \\
 $
Cancelling the common term from both the side:
$
   \Rightarrow Y = 4 - \dfrac{1}{4} \\
   \Rightarrow Y = \dfrac{{15}}{4} = 3.7m \\
 $
Hence, the depth of the lake is 3.7 m.

Note- For solving such questions related to practical application of heights and distances drawing a perfect figure is very important in order to understand the question and start the solution. Try to figure out some possible geometrical figures from the practical question. It will be easier to solve such questions when the ideal scenario is taken under consideration. Just as in the above question, we have taken the surface of the water to be straight.