Question

A ladder rests against a wall at an angle $\alpha $ to the horizontal. Its foot is pulled away from the wall through a distance ‘a’, so that it slides a distance ‘b’ down the wall making an angle $\beta $ with the horizontal. Show that: $\dfrac{a}{b}=\dfrac{\cos \alpha -\cos \beta }{\sin \beta -\sin \alpha }$.

Answer 1

Hint: First draw a rough diagram of the given situation. Assume that the length of the ladder is ‘l’. Also, assume that initially the foot of ladder is at a distance ‘x’ from the corner of the wall and after sliding the top of the ladder is at a distance ‘y’ from the corner of the wall. Use the formulas: $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$ and $\sin \theta =\dfrac{\text{Perpendicular }}{\text{Hypotenuse}}$, substitute the given values to get the simplified form.

Complete step by step answer:
According to the problem, we have a ladder resting against a wall at an angle $\alpha $ to the horizontal and its foot is pulled away from the wall through a distance ‘a’, so that it slides a distance ‘b’ down the wall making an angle $\beta $ with the horizontal. We need to prove $\dfrac{a}{b}=\dfrac{\cos \alpha -\cos \beta }{\sin \beta -\sin \alpha }$.
Let us draw the given information to get a better view.

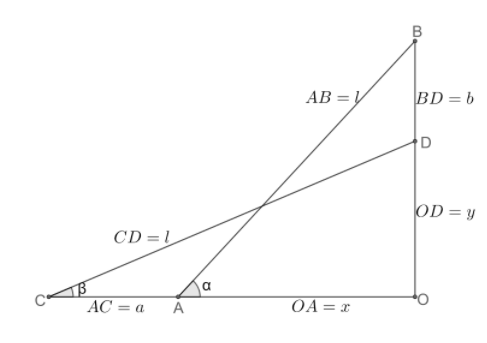
According to the above figure, we have assumed that initially the foot of the ladder is at point A which is at a distance ‘x’ from the point O. The top of the ladder is at point B.
Now, after sliding, assume that the foot of the ladder comes at point C and its top comes at point D which is at a distance ‘y’ from the point O.
The total length of the ladder is constant, which is ‘l’.
Now, in right angle triangle AOB, we have,
$AO=x$, \[OB=OD+DB=b+y\], $AB=l$, $\angle OAB=\alpha $.
We know that, $\sin \theta =\dfrac{\text{Perpendicular }}{\text{Hypotenuse}}$ and $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$. Therefore,
$\cos \alpha =\dfrac{x}{l}$.
$\Rightarrow x=l\cos \alpha ...................(i)$.
$\sin \alpha =\dfrac{b+y}{l}$.
$\Rightarrow b+y=l\sin \alpha $.
$\Rightarrow b=l\sin \alpha -y.........................(ii)$.
In right angle triangle COD we have,
$OD=y$, $OC=OA+AC=x+a$, $CD=l$, $\angle OCD=\beta $.
Now, we have $\cos \beta =\dfrac{x+a}{l}$.
$\Rightarrow x+a=l\cos \beta $.
$\Rightarrow a=l\cos \beta -x.......................(iii)$.
$\sin \beta =\dfrac{y}{l}$.
$\Rightarrow y=l\sin \beta ...........................(iv)$.
Now, we substitute the value of ‘y’ from equation (iv) in equation (ii).
$b=l\sin \alpha -l\sin \beta $.
$\Rightarrow b=l\left( \sin \alpha -\sin \beta \right)......................(v)$.
Now, we substitute the value of ‘x’ from equation (i) in equation (iii).
$a=l\cos \beta -l\cos \alpha $.
$\Rightarrow a=l\left( \cos \beta -\cos \alpha \right).......................(vi)$.
Now, we take the ratio of equation (vi) and equation (v),
\[\dfrac{a}{b}=\dfrac{l\left( \cos \beta -\cos \alpha \right)}{l\left( \sin \alpha -\sin \beta \right)}\].
\[\Rightarrow \dfrac{a}{b}=\dfrac{\left( \cos \beta -\cos \alpha \right)}{\left( \sin \alpha -\sin \beta \right)}\].
Now, we take (-1) common in both numerator and denominator.
\[\dfrac{a}{b}=\dfrac{\left( -1 \right)\left( \cos \alpha -\cos \beta \right)}{\left( -1 \right)\left( \sin \beta -\sin \alpha \right)}\].
\[\Rightarrow \dfrac{a}{b}=\dfrac{\left( \cos \alpha -\cos \beta \right)}{\left( \sin \beta -\sin \alpha \right)}\].
So, we have proved the given result $\dfrac{a}{b}=\dfrac{\cos \alpha -\cos \beta }{\sin \beta -\sin \alpha }$.

Note: We always need to remember that the length of the ladder is not going to change before and after sliding before solving this problem. We can also use tangents of the given angle to determine the different relationships but at the end we have to convert them into sine and cosine. Whenever we get this type of problem, we need to start solving by drawing the given information as the diagram gives the better view.