Answer
Verified471.6k+ views
Hint: Express the given information in the form of a right angled triangle with the ladder as its hypotenuse. Use the formula\[\cos \theta = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}{{length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\]to compute the length of the ladder.
Complete step by step answer:
Given that a ladder is leaning against a vertical wall making an angle of $60^\circ $with the ground.
The distance between the foot of the ladder and the wall is 3.5 m.
We need to find the length of this ladder.
We can view the ladder, the wall, and the ground as the sides of a triangle.
As the wall is vertical, it can be considered as one of the perpendicular sides of a right-angled triangle
Then we will have the following picture of the given information:
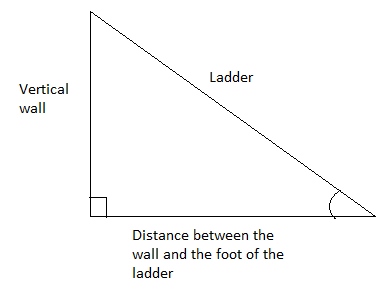
Let’s call this triangle as $\vartriangle ABC$ where side AB represents the vertical wall, side BC represents the distance between the foot of the ladder, and the wall and side AC represents the ladder.
This would imply that$\angle ACB = 60^\circ $and $BC = 3.5m$
Then according to the given information, we get the following figure:
We know that in a right angled triangle,\[\cos \theta = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}{{length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\]
Here, in$\vartriangle ABC$,$\theta = 60^\circ $, length of the adjacent side = length of side BC = 3.5 m and length of the hypotenuse = length of the ladder = length of side AC = not known.
Thus, on substituting the above values, we get
\[
\cos \theta = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}{{length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}} \\
\Rightarrow \cos 60^\circ = \dfrac{{3.5}}{{length{\text{ }}of{\text{ }}the{\text{ }}ladder}}.............(1) \\
\]
We know that$\cos 60^\circ = \dfrac{1}{2}$
On substituting$\cos 60^\circ = \dfrac{1}{2}$, we get
\[
\dfrac{1}{2} = \dfrac{{3.5}}{{length{\text{ }}of{\text{ }}the{\text{ }}ladder}} \\
\Rightarrow length{\text{ }}of{\text{ }}the{\text{ }}ladder = 3.5 \times 2 = 7m \\
\]
Hence the required length of the ladder is 7 m.
Note:
It is best to memorize the sine, cosine, and tangent values of$30^\circ $,$60^\circ $and$45^\circ $to be able to solve such questions and to avoid substitution of wrong values.
Complete step by step answer:
Given that a ladder is leaning against a vertical wall making an angle of $60^\circ $with the ground.
The distance between the foot of the ladder and the wall is 3.5 m.
We need to find the length of this ladder.
We can view the ladder, the wall, and the ground as the sides of a triangle.
As the wall is vertical, it can be considered as one of the perpendicular sides of a right-angled triangle
Then we will have the following picture of the given information:
Let’s call this triangle as $\vartriangle ABC$ where side AB represents the vertical wall, side BC represents the distance between the foot of the ladder, and the wall and side AC represents the ladder.
This would imply that$\angle ACB = 60^\circ $and $BC = 3.5m$
Then according to the given information, we get the following figure:
We know that in a right angled triangle,\[\cos \theta = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}{{length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}}\]
Here, in$\vartriangle ABC$,$\theta = 60^\circ $, length of the adjacent side = length of side BC = 3.5 m and length of the hypotenuse = length of the ladder = length of side AC = not known.
Thus, on substituting the above values, we get
\[
\cos \theta = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}{{length{\text{ }}of{\text{ }}the{\text{ }}hypotenuse}} \\
\Rightarrow \cos 60^\circ = \dfrac{{3.5}}{{length{\text{ }}of{\text{ }}the{\text{ }}ladder}}.............(1) \\
\]
We know that$\cos 60^\circ = \dfrac{1}{2}$
On substituting$\cos 60^\circ = \dfrac{1}{2}$, we get
\[
\dfrac{1}{2} = \dfrac{{3.5}}{{length{\text{ }}of{\text{ }}the{\text{ }}ladder}} \\
\Rightarrow length{\text{ }}of{\text{ }}the{\text{ }}ladder = 3.5 \times 2 = 7m \\
\]
Hence the required length of the ladder is 7 m.
Note:
It is best to memorize the sine, cosine, and tangent values of$30^\circ $,$60^\circ $and$45^\circ $to be able to solve such questions and to avoid substitution of wrong values.