Question

A Gulab jamun, contains sugar syrup up to about 30% of its volume. Find the approximately how much syrup would be found in 45 Gulab jamuns each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
                   

Answer 1

Hint: To solve this question, we will use some basic formulae of surface area and volumes of figures. We have to remember that the volume of cylinder with height h and radius r is given by $\pi {r^2}h$ and volume of hemisphere is given by $\dfrac{2}{3}\pi {r^3}$

Complete step-by-step answer:
Given that,
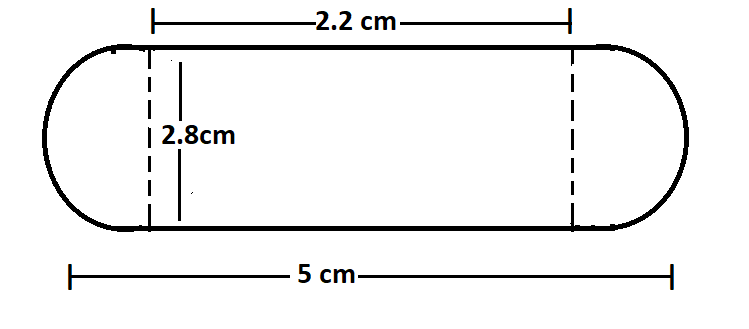
Length of Gulab jamun = 5cm.
Diameter of hemispherical ends = 2.8cm.
So,
Radius of hemisphere = $\dfrac{{2.8}}{2} = 1.4cm$
We know that,
Volume of hemisphere = $\dfrac{2}{3}\pi {r^3}$
So, the volume of the hemispherical end of the Gulab jamun will be,
$ \Rightarrow \dfrac{2}{3} \times \dfrac{{22}}{7} \times {\left( {1.4} \right)^3}$
$ \Rightarrow 5.75c{m^3}$
According to the question, there are two hemispherical ends in the Gulab jamun.
So, the total volume of the hemispherical ends = $2 \times $volume of hemispherical end.
$ \Rightarrow 2 \times 5.75c{m^3}$
$ \Rightarrow 11.5c{m^3}$
Here, the height of the cylindrical part of the Gulab jamun will be given as,
$ \Rightarrow $ length of Gulab jamun – ( $2 \times $radius of hemispherical end )
$ \Rightarrow 5 - \left( {2 \times 1.4} \right)$
$ \Rightarrow 5 - \left( {2.8} \right)$
$ \Rightarrow 2.2cm$
We know that, volume of cylinder = $\pi {r^2}h$
So, the volume of the cylindrical part of Gulab jamun is,
$ \Rightarrow \dfrac{{22}}{7} \times {\left( {1.4} \right)^2} \times 2.2$
$ \Rightarrow 13.55c{m^3}$
Therefore, the total volume of the Gulab jamun = volume of cylindrical part + volume of hemispherical part
$ \Rightarrow V = 11.5 + 13.55$
$ \Rightarrow V = 25.05c{m^3}$
According to the question, 30% of the volume of Gulab jamun is the sugar syrup.
So, the volume of sugar syrup in 1 Gulab jamun = $\dfrac{{30}}{{100}} \times V$
$ \Rightarrow \dfrac{{30}}{{100}} \times 25.05c{m^3}$
$ \Rightarrow 7.515c{m^3}$
Therefore,
The sugar syrup in 45 Gulab jamun = $45 \times 7.515c{m^3}$
$ \Rightarrow 338.175c{m^3}$
Hence, we can say that the approximate volume of sugar syrup in 45 Gulab jamuns is $338c{m^3}$

Note: In this type of questions, we should know the formula of volume of cylinder and hemisphere. First, we will find out the volume of 1 Gulab jamun by considering the both cylindrical and hemispherical part. Then, we will find the volume of sugar syrup in 1 Gulab jamun by doing 30% of it. After that, we will multiply that volume with 45 and we will get the required volume of sugar syrup.