Question

A girl is on the beach with her father. She spots a swimmer drowning. She shouts to her father who is 50 m due west of her. Her father is 10 m nearer to a boat than the girl. If her father uses the boat to reach the swimmer, he has to travel a distance 126 m from that boat. At the same time, the girl spots a man riding a watercraft who is 98 m away from the boat. The man on the water craft is due east of the swimmer. How far must the man travel to rescue the swimmer?

Answer 1

Hint: Use the property of similarity of triangles to solve this problem
Two triangles are similar if at least two angles of one triangle are equal to any two angles of the other triangle; this is known as Angle-Angle (AA) similarity.
Two triangles are similar if any two sides of the triangles are in proportion and the angles between those sides are equal; this is known as Side-Angle-Side (SAS) similarity.

Complete step by step solution:
According to the question we get the required figure

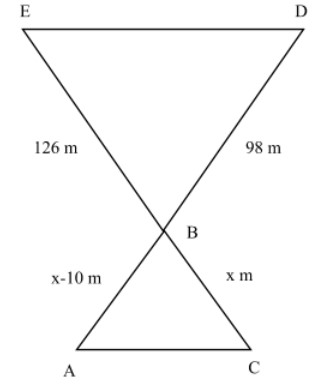
Let A be the place where her father is standing
B is the position of boat
C is the place where girl is standing
D is the position of watercraft
E is the position of swimmer
Here we have to find the distance ED
Here, BC = x meter; AB = (x-10) meter
Consider ∆ABC and ∆DBE
$\angle ABC = \angle DBE$ (Vertically opposite angles)
$\angle BAC = \angle BDE$ (Alternate angles)
Using AA similarity, $\Delta ABC \sim \Delta DBE$
$\dfrac{{AB}}{{DB}} = \dfrac{{BC}}{{BE}} = \dfrac{{AC}}{{ED}}$
So,$\dfrac{{AB}}{{DB}} = \dfrac{{BC}}{{BE}}$
From the figure
$\begin{gathered}
  \dfrac{{x - 10}}{{98}} = \dfrac{x}{{126}} \\
  126x - 1260 = 98x \\
  28x = 1260 \\
  x = 45m \\
\end{gathered} $
∴BC = 45 m
Also, $\dfrac{{BC}}{{BE}} = \dfrac{{AC}}{{ED}}$
$\begin{gathered}
  ED = \dfrac{{AC \times BE}}{{BC}} \\
  ED = \dfrac{{50 \times 126}}{{45}} \\
  ED = 140m \\
\end{gathered} $
∴Man has to travel 140 m to rescue the swimmer

Note: The similarity of any two triangles can be proved by using any other postulates also provided they satisfy the given condition of similarity.