Question

A cuboid dimension 5 cm 4 cm 2 cm. Number of cubes of 2 cm side that can be cut from cuboid is:
(a) 18
(b) 5
(c) 10
(d) None of these

Answer 1

Hint: To find the number of cubes that can be formed from the cuboid, we need to keep in mind that the volume of the figures will be the same as no material goes to the waste. This means, the volume of the cuboid will be the same as that of the sum of the volumes of the cubes. We will find the volume of the cuboid, given by the product if length, breadth and height of the cuboid. To find the volume of the cube, we need to find the cube of the given length of a side. Thus, to find the number of cubes formed, we have to find the quotient of volume of cuboid and volume of cube.

Complete step-by-step answer:
Following is the diagram of the cuboid.

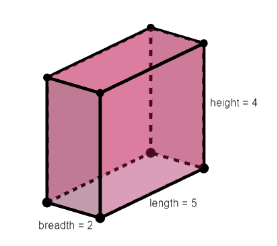
The dimensions of the cuboid are given as 5 cm 4 cm 2 cm. This means, length of the cuboid is 5 cm, breadth is 4 cm and height is 2 cm.
The volume of a cuboid is given as the product of its length, breadth and height.
Thus, volume of the cuboid = 5x4x2 = 40 cu. cm
It is also given that the length of a side of the cube is 2 cm.
The volume of the cube is given as the cube of the length of a side of that cube.
Thus, the volume of each cube will be = $ {{2}^{3}} $ = 8 cu. cm
This means that each cube will require 8 cu. cm of the material and we have 40 cu. cm of material available.
So, the number of cubes will be quotient of volume of cuboid and volume of cube.
Thus, number of cubes = $ \dfrac{40}{8} $ = 5
Therefore, the number of cubes formed is 5.
So, the correct answer is “Option B”.

Note: Students are advised to always remember that the conservation of mass is always true and thus the total volume will never change. Either it will be used to form a new solid completely or a fraction of the volume is used to form solid and the remaining volume of material is used for other work, but the mass and hence volume will always be conserved.