Question

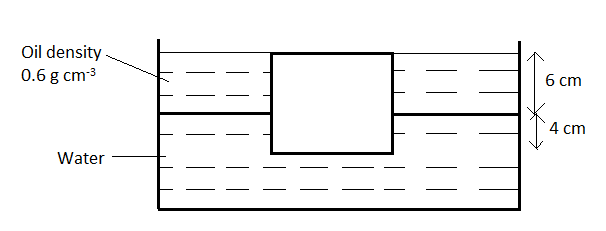
A cubical block of wood $10cm$ on a side floats at the interface of oil and water as shown in the figure. The density of oil is $0.6g.c{{m}^{-3}}$ and density of water is $1g.c{{m}^{-3}}$. The mass of the block is
 

A. $706\text{ }g$
B. $607\text{ }g$
C. $760\text{ }g$
D. $670\text{ }g$

Answer 1

Hint: This problem can be solved by using Archimedes’ principle, which states that when an object is immersed partially or completely in a fluid, it experiences an upward buoyant force, that is, equal to the weight of the fluid. Since, the block is at equilibrium its weight must be equal in magnitude to the upward buoyant forces exerted by the two liquids. By finding out the buoyant forces of the two liquids, we can find out the weight of the block and hence, the mass of the block.

Formula used:
${{F}_{B}}=-{{W}_{liquid}}$ (Archimedes’ principle)
where ${{F}_{B}}$ is the buoyant force experienced by a body in a fluid and ${{W}_{liquid}}$ is the weight of the fluid displaced by the body. The negative sign implies that the buoyant force acts opposite in direction to the weight of the body.
$\text{Mass = Density}\times \text{Volume}$
For a body in static equilibrium the sum of the forces $\left( \overrightarrow{F} \right)$ on it are zero.
$\therefore \sum{\overrightarrow{F}}=0$

Complete step by step answer:
In the figure given, the block is floating with part of its volume in water and part in oil. Since, it is in equilibrium, the sum of the buoyant forces provided to it by the two liquids must be balancing the weight of the body. Hence, we can find the mass of the block by finding the sum of the buoyant forces and equating it to the weight (which is nothing but the product of the mass and the acceleration due to gravity).
To find the buoyant forces provided by the two liquids, we will make use of Archimedes’ principle, which states that when an object is immersed partially or completely in a fluid, it experiences an upward buoyant force, that is, equal to the weight of the fluid.
${{F}_{B}}=-{{W}_{liquid}}$ (Archimedes’ principle) -(1)
where ${{F}_{B}}$ is the buoyant force experienced by a body in a fluid and ${{W}_{liquid}}$ is the weight of the fluid displaced by the body. The negative sign implies that the buoyant force acts opposite in direction to the weight of the body.
Now, let us analyze the question.
Let the volume of water displaced be ${{V}_{water}}$.
Let the volume of oil displaced be ${{V}_{oil}}$.
Now, let the cross sectional area of the block be $A$.
$\therefore A=\text{sid}{{\text{e}}^{2}}={{\left( 10cm \right)}^{2}}=100c{{m}^{2}}$ (Since, the side of the block is $10cm$)
Now, since,
$\text{Volume = Cross sectional Area}\times \text{height}$,
we get,
${{V}_{water}}=A\times 4=100\times 4=400c{{m}^{3}}$ --(2)
Similarly, we get,
${{V}_{oil}}=A\times 6=100\times 6=600c{{m}^{3}}$ --(3)
Let the density of water be ${{\rho }_{water}}=1g.c{{m}^{-3}}$.
Let the density of oil be ${{\rho }_{oil}}=0.6g.c{{m}^{-3}}$.
Now, since $\text{Mass = Density}\times \text{Volume}$, we get,
${{M}_{water}}={{V}_{water}}\times {{\rho }_{water}}=400\times 1=400gm$ --(4)
where ${{M}_{water}}$ is the mass of the water displaced.
Similarly,
${{M}_{oil}}={{V}_{oil}}\times {{\rho }_{oil}}=600\times 0.6=360gm$ ---(5)
where ${{M}_{oil}}$ is the mass of the oil displaced.

Let the weight of the water displaced be ${{W}_{water}}$.
Now,
${{W}_{water}}={{M}_{water}}g$ --(6)
where ${{M}_{water}}$ is the mass of the water displaced and $g$ is the acceleration due to gravity.
Similarly,
${{W}_{oil}}={{M}_{oil}}g$ --(7)
where ${{M}_{oil}}$ is the mass of the oil displaced and $g$ is the acceleration due to gravity.
Now, since the block is floating in the liquid, it is in static equilibrium. Therefore the sum of the vertical forces on it must be zero.
For a body in static equilibrium the sum of the forces $\left( \overrightarrow{F} \right)$ on it are zero.
$\therefore \sum{\overrightarrow{F}}=0$ --(8)
Now, the vertical forces on the block are its own weight $Mg$ downward, where $M$ is its mass and the upward buoyant forces from oil and water.
Considering upward forces as positive and using (8), we get,
${{W}_{water}}+{{W}_{oil}}-Mg=0$
Using (6) and (7), we get,
${{M}_{water}}g+{{M}_{oil}}g=Mg$
$\therefore M={{M}_{oil}}+{{M}_{water}}=360+400=760gm$ (Using (4) and (5))
Hence, the mass of the block is $760gm$.
Therefore, the correct option is C) $760\text{ }g$.

Note: Students often get confused upon seeing more than one fluid in the problem and think what would be the value of the upthrusts and whether both the fluids will provide buoyant forces. They must remember the basic Archimedes’ principle and thus realize that the block displaces a certain volume of both the liquids and hence both the liquids will provide their respective buoyant forces equal to the weights of the respective liquid displaced. Proceeding in this way and finding out the individual buoyant forces due to each liquid and summing them up in the end as required, is the best way of attempting such questions.