Question

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m and is inclined at an angle of ${30^ \circ }$to the ground, whereas for the elder children, she wants to have a steep slide at a height of 3 m and inclined at an angle of ${60^ \circ }$ to the ground. What should be the length of the slide in each case?

Answer 1

Hint: Consider a different right angled triangle for both the cases. Use a suitable trigonometric ratio to evaluate the value.

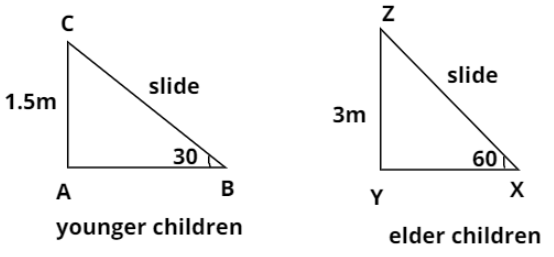
For slides of younger children, consider the first triangle, $\Delta ABC$.
AC is the height of the top of the slide from the ground and it is 1.5 m (given in the question).
Angle of inclination of the slide to the ground is ${30^ \circ }$ so $\angle ABC = {30^ \circ }$. We have to calculate the length of the slide i.e. BC. So in $\Delta ABC$:
$
   \Rightarrow \sin {30^ \circ } = \dfrac{{AC}}{{BC}}, \\
   \Rightarrow \dfrac{1}{2} = \dfrac{{1.5}}{{BC}}, \\
   \Rightarrow BC = 3 \\
$
Thus, the length of the slide in this case is 3 m.
Next for slides of younger children, consider $\Delta XYZ$
YZ is the height of the top of the slide from the ground and it is 3 m (given in the question).
Angle of inclination of the slide to the ground is ${60^ \circ }$ so $\angle YXZ = {60^ \circ }$. We have to calculate the length of the slide i.e. XZ. So in $\Delta XYZ$:
$
   \Rightarrow \sin {60^ \circ } = \dfrac{{YZ}}{{XZ}}, \\
   \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{3}{{XZ}}, \\
   \Rightarrow XZ = \dfrac{{3 \times 2}}{{\sqrt 3 }}, \\
   \Rightarrow XZ = 2\sqrt 3 \\
$
Thus, the length of the slide in this case is $2\sqrt 3 $ m.
Note: In the above two scenarios, perpendicular was known to us and we were required to calculate hypotenuse. Trigonometric ratio concerning these two sides is $\sin \theta $. That’s why we used it. In different scenarios, we can use different trigonometric ratio as per the convenience.