Question

A conical solid block is exactly fitted inside the cubical box of side ‘a’ then the volume of the conical solid block is $\dfrac{{4\pi {a^{3n}}}}{3}$. Is this statement true? Justify your answer.

Answer 1

Hint: In this problem we will first find the volume of the solid cone and the volume of the cubical box to check if the given statement is true or false.

Complete step-by-step answer:
Now, we will first calculate the volume of the cubical box. The side of cubical box is a, so the volume of cubical box,
Volume of cubical box = ${(side)^3}$ = ${a^3}$.

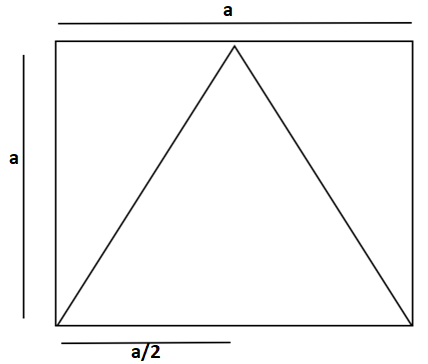
Now, according to the question, if the solid conical block is exactly fitted inside the cubical box, then we can see that the radius (r) = $\dfrac{a}{2}$ and height (h) = a.
So, volume of conical solid block = $\dfrac{{\pi {r^2}h}}{3}$ = $\dfrac{{\pi {{\left( {\dfrac{a}{2}} \right)}^2}a}}{3}$ = $\dfrac{{\pi {a^3}}}{{12}}$.
So, the given statement is not true because, the given volume of conical block is greater than the volume of cubical block in which the conical block is fitted which is not possible. The correct volume of solid conical block fitted inside the box is $\dfrac{{\pi {a^3}}}{{12}}$.

Note: In such a type of question first check whether the given statement is true or not by finding the exact volume. It is also very important that you read the question properly to find the correct parameters to find the volume. Apply the exact formula to get the correct answer.