Question

A company manufactures three kinds of calculators: A, B and C in its two factories 1 and 2. The company has got an order for manufacturing at least 6400 calculators of kind A, 4000 of kind B and 4800 of kind C. The daily output of factory 1 is of 50 calculators of kind A, 50 calculators of kind B and 30 calculators of kind C. The daily output of factory 2 is of 40 calculators of kind A, 20 of kind B and 40 of kind C. The cost per day to run factory 1 is Rs. 12000 and of factory 2 is Rs.15000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically.

Answer 1

Hint: For solving this problem, we should be aware about the basic concepts concerning Linear Programming problems. We will formulate the above problem in terms of two variables (x and y) to represent the above given problem. Here, x represents the number of days factory 1 runs and y represents the number of days factory 2 runs. These equations are then plotted on a graph and then we get the required points where value of cost is evaluated.

Complete step-by-step answer:

Now, to solve the problem, we try to represent the constraints given in the problem using x and y, where, x represents the number of days factory 1 runs and y represents the number of days factory 2 runs. Thus, from first condition which states that company has to manufacture at least 6400 calculators of kind A, 4000 of kind B and 4800 of kind C. Further, given the daily output of factory 1 is of 50 calculators of kind A, 50 calculators of kind B and 30 calculators of kind C and the daily output of factory 2 is of 40 calculators of kind A, 20 of kind B and 40 of kind C, we have, following equations,
50x + 40y $\ge $ 6400 -- (1)
50x + 20y $\ge $ 4000 -- (2)
30x + 40y $\ge $ 4800 -- (3)
We also know that the number of days factory 1 and factory 2 run is a positive quantity. Thus, we have,
x $\ge $ 0 -- (4)
y $\ge $ 0 -- (5)
Now, to minimize cost, it is given that the cost per day to run factory 1 is Rs. 12000 and of factory 2 is Rs.15000. Thus, we have,
f(x,y) = 12000x + 15000y -- (A)
Now, we represent (1), (2), (3), (4) and (5) on the graph, we have,

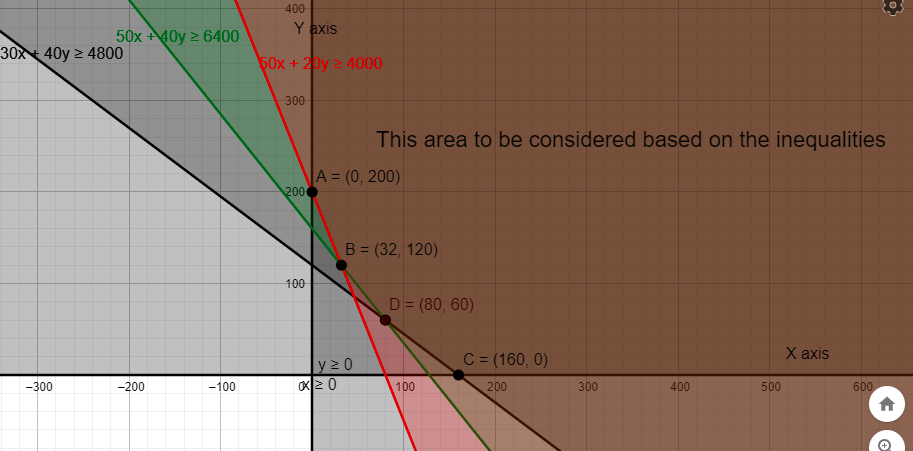
To find the minimum cost we will find the cost of function at the vertices A (0,200), B (32, 120), C (80,60) and D (160,0) as shown on the graph. Point B is obtained by intersection of lines (1) and (2), while point D is obtained by intersection of lines (1) and (3). To find B, we solve 50x + 40y = 6400 and 50x + 20y = 4000. Thus, solving them, we will get x = 32 and y = 120. To find C, we solve 50x + 40y = 6400 and 30x + 40y = 4800. Thus, solving them, we will get x = 80 and y = 60.
Now, we find the cost at each of these points. We have,
Case 1: (0,200)
f(x,y) = 12000x + 15000y
f(0,200) = 12000 $\times $ 0 + 15000 $\times $ 200
f (0,200) = 3000000
Case 2: (32,120)
f(x,y) = 12000x + 15000y
f(0,200) = 12000 $\times $ 32 + 15000 $\times $ 120
f (0,200) = 2184000
Case 3: (80,60)
f(x,y) = 12000x + 15000y
f(0,200) = 12000 $\times $ 80 + 15000 $\times $ 60
f (0,200) = 1860000
Case 4: (160,0)
f(x,y) = 12000x + 15000y
f(0,200) = 12000 $\times $ 160 + 15000 $\times $ 0
f (0,200) = 1920000
Thus, from this, we can say that minimum cost occurs at (80, 60) with cost as Rs 1860000. Since, the region is unbounded, we check if 12000x + 15000y < 1860000. (represented by dashed blue line)

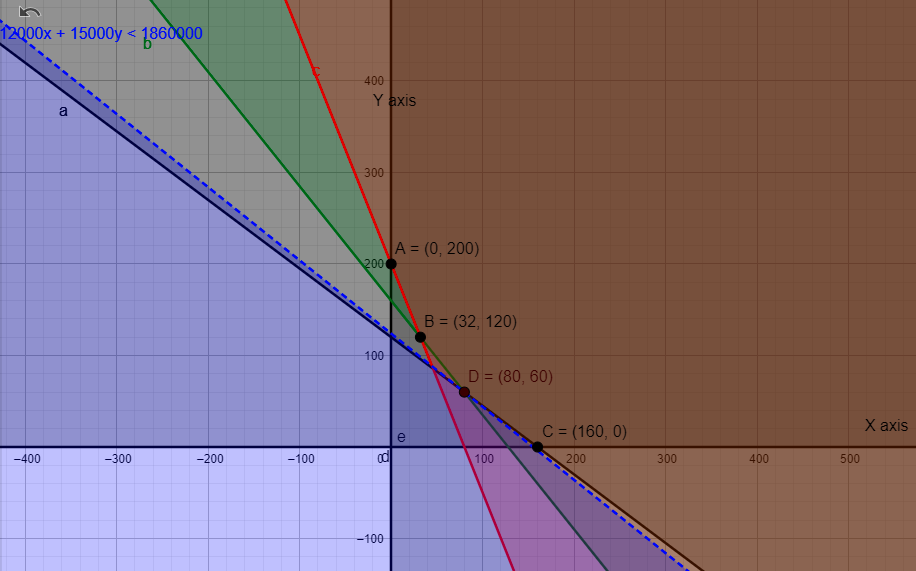
The area 12000x + 15000y < 1860000 represents is the blue color figure in the graph. Clearly, there is no part in common with the feasible solution of our problem, thus we can successfully conclude that Rs 1860000 is indeed the minimum cost and this occurs for factory 1 operating for 80 days and factory 2 for 60 days.

Note: While solving LPP (Linear Programming Problems), it is always important not to forget the trivial cases (like in this problem, we had x $\ge $ 0 and y $\ge $ 0). Another, key point to note is that the graphical method can only be effectively used for solving problems concerning two variables. Suppose, we had a third constraint concerning another variable (say z), then, it becomes a 3-dimensional problem making it much more tedious to solve by graph. In such cases, generally we use a software like Matlab to solve these types of problems.