Question

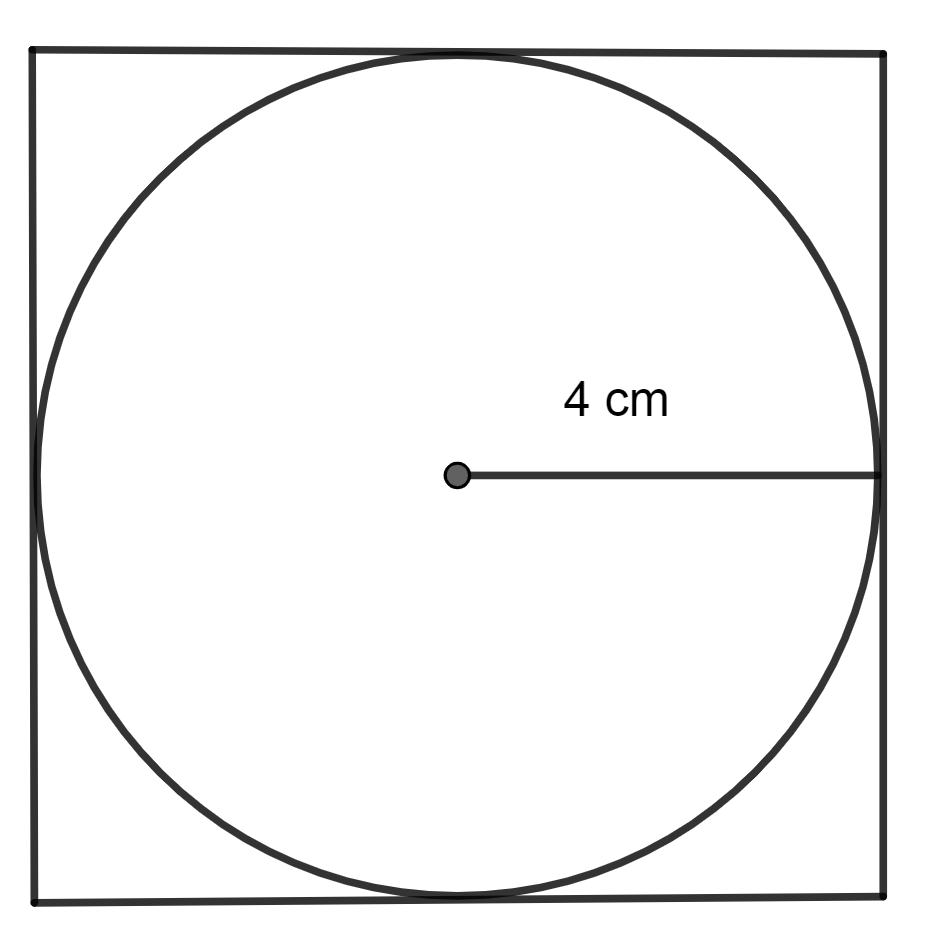
A circle is inscribed in a square as shown. If the radius of the circle is 4cm, then the perimeter of the square is

A. 28 cm
B. 24 cm
C. 32 cm
D. 36 cm

Answer 1

Hint: At first, use the given radius of the circle to find its diameter by multiplying it with 2. Then, use the property that the diameter of the circle is the length of the side of the square. Hence, find the perimeter of square by using formula, \[\text{Perimeter}=4\times \text{length of side of square}\]

Complete step by step answer:
In the question, we are given a figure in which a circle is inscribed in a square, where the radius of the inscribed circle is given and we have to find the perimeter of the square from the given data.
So, the figure is,

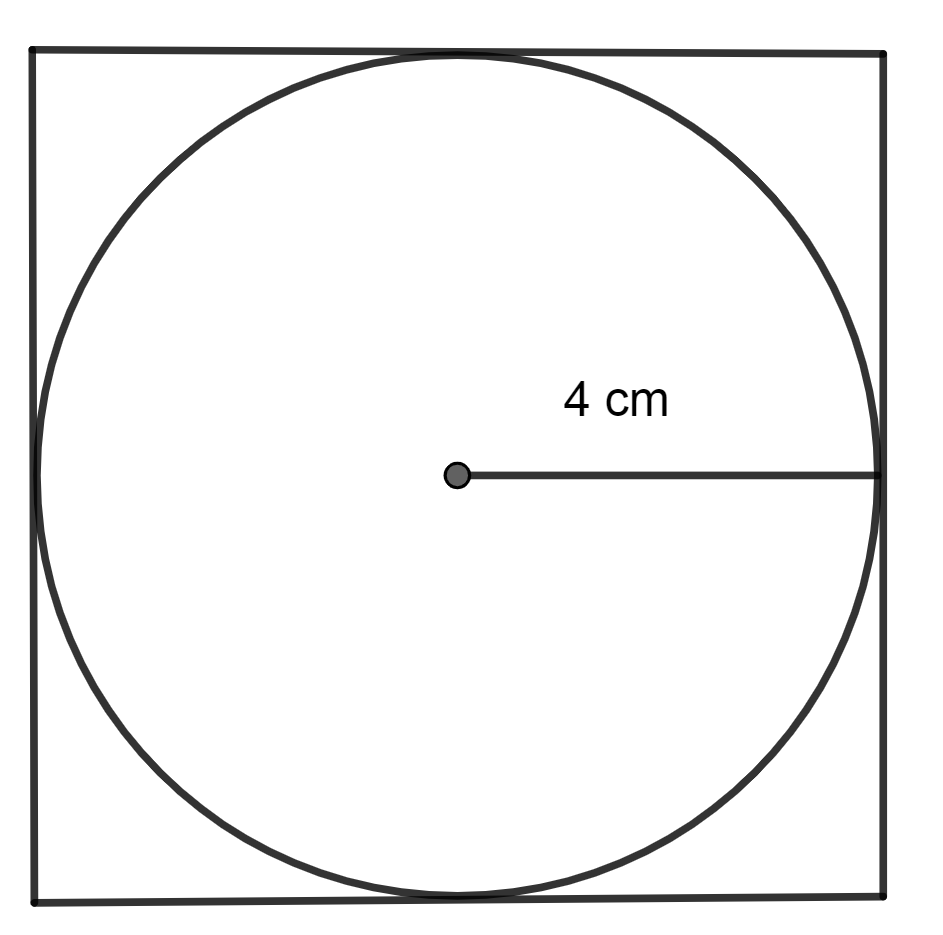
Now, as we know that the circle is touching each of the sides of the circle, we can say that the length of the side of the circle is equal to the length of the circle's diameter.
We know that the length of the radius of the circle is 4cm. So, we can find out the diameter by using the fact that the length of the diameter of the circle is twice the length of the radius.
So, as the radius is 4cm, then, the diameter will be \[2\times 4cm\Rightarrow 8cm.\]
So, the length of the side of the square will be 8cm.
Now, as we know, the length of the side of the square which is 8cm, then, we can find its perimeter by using formula, \[\text{Perimeter= 4}\times \text{l}\] where l represents the length of the side of a square.
So, the perimeter will be \[4\times 8cm\Rightarrow 32cm\]

So, the correct answer is “Option C”.

Note: The question was the case in which the circle was inscribed in square. Now, we will see the case where the square was inscribed. Here, the figure will be:

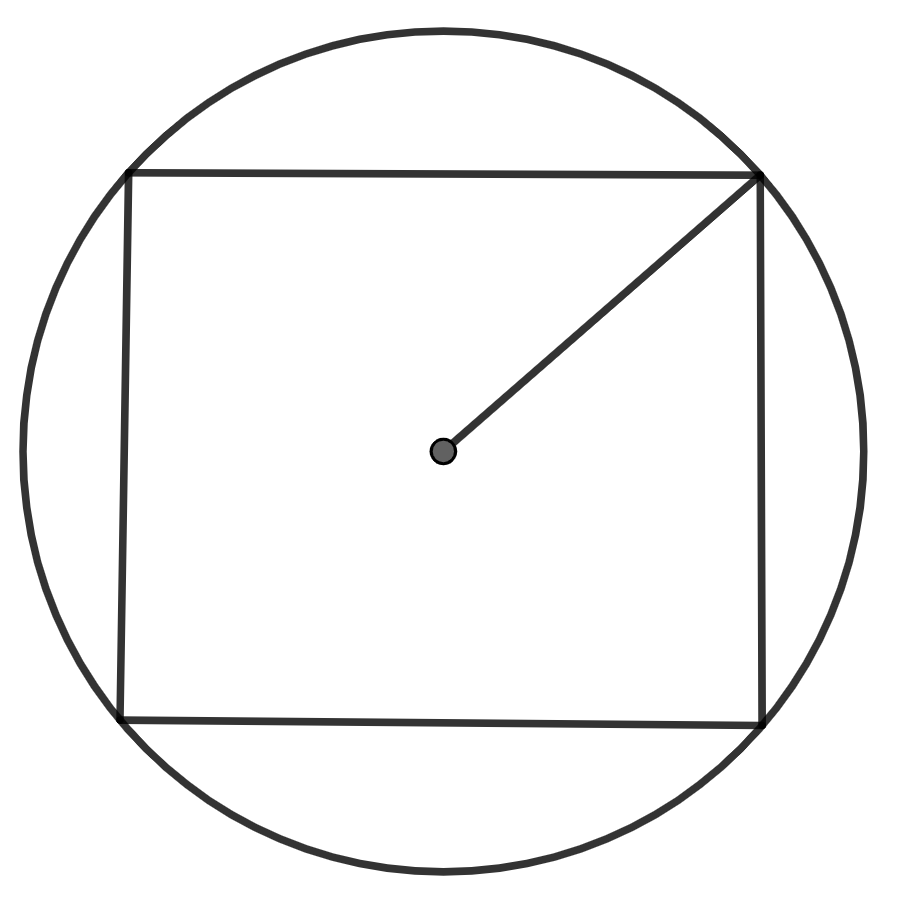
In this, we will use the property that, length of the diagonal equals the diameter of the square, if the radius of the circle is given or vice versa.
While solving this question, students must note that we have been asked to find the perimeter of the square, so they can remember the fact that the side length of a square with an inscribed circle will be the diameter of that circle.