Question

A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and a height of 2m. If the outer side of each of the cones is to be painted and the cost of painting is 12 per \[{{m}^{2}},\] what will be the cost of painting all these cones.

Answer 1

Hint: We are given the dimensions of the cone as diameter, D = 40 cm, height, h = 2m. So, we have to find the curved surface area using the formula \[S=\pi rl.\] For that, we have to calculate the value of slant height (l) by using the formula \[l=\sqrt{{{h}^{2}}+{{r}^{2}}}.\] When we have the area of one cone, we will multiply \[50\times S\] to find the total area and at last, we will find the total cost by multiplying the area by 12.

Complete step-by-step answer:
We are given that the bus stop is barricaded using 50 hollow cones. We have to find the cost of painting these barricades. In order to find the cost, first, we have to find the total surface area of the cone. We know that the curved surface area of the cone is given as \[S=\pi rl,\] where r is the radius, and l is the slant height.

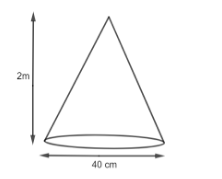
Now, we are given that the diameter is 40cm. From this, we can find the radius by using the formula,
\[r=\dfrac{D}{2}\]
\[\Rightarrow r=\dfrac{40}{2}\]
\[\Rightarrow r=20cm\]
So, we have the radius as 20cm.
Also, we need to find the slant height. We know that slant height l is given by
\[l=\sqrt{{{h}^{2}}+{{r}^{2}}}\]
We have h = 2m = 200cm and r = 20 cm.
So,
\[l=\sqrt{{{\left( 200 \right)}^{2}}+{{\left( 20 \right)}^{2}}}\]
\[\Rightarrow l=\sqrt{40000+400}\]
\[\Rightarrow l=\sqrt{40400}\]
\[\Rightarrow l=201\left( approx \right)\]
Now, we will look for the surface area of the single cone.
\[S=\pi rl\]
\[\Rightarrow S=\dfrac{22}{7}\times 20\times 201\]
Solving further, we get,
\[S=12634.285c{{m}^{2}}\]
We are given that we have 50 such cones. So, the total surface to be painted will be
\[\text{Total Surface to be Painted}=50\times \text{Surface Area of 1 cone}\]
\[\Rightarrow \text{Total Surface to be Painted}=50\times S\]
\[\Rightarrow \text{Total Surface to be Painted}=50\times 12634.285\]
\[\Rightarrow \text{Total Surface to be Painted}=631714.28c{{m}^{2}}\]
We are given that the cost of painting is Rs. 12 per \[{{m}^{2}}.\]
So, we have to convert the surface area into \[{{m}^{2}}.\] We know that,
\[1{{m}^{2}}=10000c{{m}^{2}}\]
\[\Rightarrow 10000c{{m}^{2}}=1{{m}^{2}}\]
So by the unitary method, we will get,
\[\Rightarrow 1c{{m}^{2}}=\dfrac{1}{10000}{{m}^{2}}\]
Now, we will convert \[631714.28c{{m}^{2}}\] into \[{{m}^{2}}.\]
\[631714.28c{{m}^{2}}=\dfrac{631714.28}{10000}\]
\[\Rightarrow 631714.28c{{m}^{2}}=63.17{{m}^{2}}\]
So, in \[{{m}^{2}}\] we have our total areas as \[63.17{{m}^{2}}.\]
Now, we have the cost of \[1{{m}^{2}}\] as Rs. 12. Therefore by using the unitary method, we get,
\[\text{Cost of }63.17{{m}^{2}}=12\times 63.17\]
\[\Rightarrow \text{Cost of }63.17{{m}^{2}}=Rs.758.04\]
So, we have the cost of painting all the cones as Rs. 758.04.

Note: You can also convert the dimension into m from the very starting so that you do not have to convert the area into \[{{m}^{2}}.\] While finding the slant height (l), we have to be very careful as adding two squares and finding its roots can sometimes lead to a mistake in calculation.