Question

A bucket made of aluminium sheet is of height \[20cm\] and its upper and lower ends are of radius \[25cm\] and \[10cm\] respectively. Find the cost of making the bucket if the aluminium sheet costs \[Rs.70\] per \[100c{m^2}{\text{.}}\left( {{\text{Use }}\pi = 3.14} \right)\]

Answer 1

Hint: - The bottom part is in the shape of a circle.So, Area of circle $ = \pi {r^2}$ and Lateral surface area of Frustum of cone \[ = \pi \left( {R + r} \right)\sqrt {{{\left( {R - r} \right)}^2} + {h^2}} \]

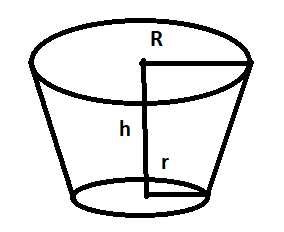
Let assume
Height of frustum of cone\[h = 20\;cm\]
Radius of upper end \[R = 25\;cm\]
Radius at bottom end \[r = 10\;cm\]
Here in this question to find the area of aluminium sheet used for making the bucket, we have to find the total surface area of frustum of cone.
Total surface area = curved surface area + area of bottom circle
\[ \Rightarrow \pi \left( {R + r} \right)\sqrt {{{\left( {R - r} \right)}^2} + {h^2}} + \pi {r^2}\]
Take$\pi $common so that the equation simplifies
\[ \Rightarrow \left( {\left( {R + r} \right)\sqrt {{{\left( {R - r} \right)}^2} + {h^2}} + {r^2}} \right)\pi \]
Now put the value of all variables in above equation
\[
   \Rightarrow \left( {\left( {25 + 10} \right)\sqrt {{{\left( {25 - 10} \right)}^2} + {{20}^2}} + {{10}^2}} \right)\pi \\
   \Rightarrow \left( {\left( {35} \right)\sqrt {{{\left( {15} \right)}^2} + 400} + 100} \right)\pi \\
\]
Simplify it further, such that
\[
   \Rightarrow \left( {\left( {35} \right)\sqrt {225 + 400} + 100} \right)\pi \\
   \Rightarrow \left( {\left( {35} \right)\sqrt {625} + 100} \right)\pi \\
   \Rightarrow \left( {\left( {35} \right) \times 25 + 100} \right)\pi \\
   \Rightarrow \left( {875 + 100} \right) \times 3.14 \\
   \Rightarrow 3061.5c{m^2} \\
\]
Thus, the total aluminium sheet required for making the bucket \[ = 3061.5\;c{m^2}\]
cost of \[100\;c{m^2}\] aluminium sheet which is given\[ = 70\;Rs.\]
therefore, cost of \[1c{m^2}\]aluminium sheet \[ = \dfrac{{70}}{{100}} = 0.7\;Rs.\]
from the cost of \[3061.5\;c{m^2}\] aluminium sheet \[ = 3061.5 \times 0.7 = 2143.05\;Rs.\]
Hence the cost of making the bucket is \[2143.05\;Rs.\]
Note: - Bucket is nothing but a frustum of cone. For a question like this, always first focus on what is given in the question itself. Total surface area is equal to curved surface area plus area of bottom circle. Remember basic formulas like area of circle $ = \pi {r^2}$and Lateral surface area of Frustum of cone\[ = \pi \left( {R + r} \right)\sqrt {{{\left( {R - r} \right)}^2} + {h^2}} .\]