Question

A boy standing on a horizontal plane finds a bird, flying at a distance of 100 m from him at an elevation of ${{30}^{\circ }}$. A girl standing on the roof of a 20 m high building finds the angle of elevation of the same bird to be ${{45}^{\circ }}$. Both the boy and the girl are on the opposite side of the bird. Find the distance of the bird from the girl.

Answer 1

Hint: Draw a diagram of the given situation and use sine of the angles given, to determine the distance of the bird from the girl. The diagram of the situation mainly consists of right angle triangles.

Complete step-by-step answer:

The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. For example, if we are standing on the ground and looking at the top of a tower then the angle subtended between the horizontal line and the line of sight is called angle of elevation.
Now, we come to the question. Let us assume that the boy is standing at point B, girl at G and bird is at point A. The tower on which the girl is standing is GN, where N is the base of the tower. We know that, $\sin \theta =\dfrac{perpendicular}{Hypotenuse}$.

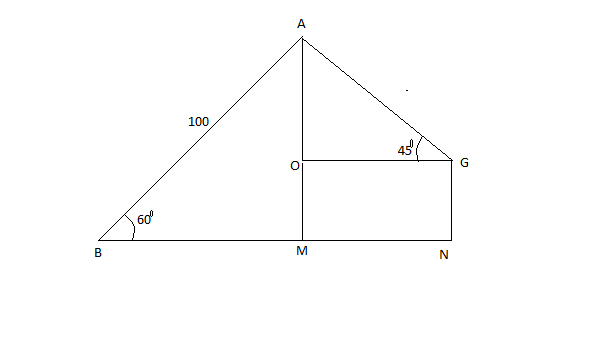
In triangle ABM,
$\begin{align}
  & \sin {{30}^{\circ }}=\dfrac{AM}{AB} \\
 & \dfrac{1}{2}=\dfrac{AM}{100} \\
 & \therefore AM=50\text{ m} \\
\end{align}$
Now, $GN=OM=20\text{ m}$, where GN is the height of the tower and OM is the side opposite to GN in the rectangle OMNG. Therefore, the length of $AO$$=AM-OM=50-20=30\text{ m}$.
In triangle AOG,
$\begin{align}
  & \sin {{45}^{\circ }}=\dfrac{AO}{AG} \\
 & \dfrac{1}{\sqrt{2}}=\dfrac{30}{AG} \\
 & \therefore AG=30\sqrt{2}\text{ m} \\
\end{align}$
Hence, distance of the girl from the bird $=AG=30\sqrt{2}\text{ m}$.

Note: It is important to draw the diagram of the given situation because diagrams will help us to solve the question more easily as compared to just imagining and solving. Also, sine of the angle is used because we had to find the hypotenuse of the right angle triangle and the length of perpendicular was given to us.