Question

A body of mass m is moving with constant velocity v along a line parallel to the x-axis. The angular momentum with respect to the origin is
A) Remains constant.
B) Is zero.
C) Goes on decreasing.
D) Goes on increasing.

Answer 1

Hint: The angular momentum is defined as the product of its moment of inertia and its angular velocity. It is analogous to linear momentum. In formula it is written as $\mathop L\limits^ \to $ =$\mathop r\limits^ \to \times \mathop p\limits^ \to $ where $\mathop L\limits^ \to $ denotes angular momentum, $\mathop r\limits^ \to $ is the perpendicular distance and $\mathop p\limits^ \to $ is the momentum. Here mass and velocity is constant.

Complete step by step solution:
Step 1:
A body of mass $M$ is moving with constant velocity $v$ parallel to the $x$-axis. Let the perpendicular distance between the x-axis and the path of the particle is r.

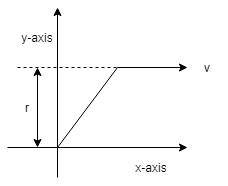
Step 2:
Then the angular momentum of the body about x-axis is given by, $\mathop L\limits^ \to $ =$\mathop r\limits^ \to \times \mathop p\limits^ \to $
where, $\mathop r\limits^ \to $ is the perpendicular distance between the path of the particle and x-axis, and $\mathop p\limits^ \to $ is the linear momentum of the particle. The momentum of a particle depends on the product of its mass and velocity. From the above diagram, we can observe that the perpendicular distance $r$ and velocity are perpendicular to each other. We have velocity, mass, and perpendicular distance all are constant. So angular momentum $\mathop L\limits^ \to $ will be constant.

$\therefore$ The angular momentum $\mathop L\limits^ \to $ will be constant. Hence, option (A) is correct.

Note:
Alternate method:
This method is similar to the previous one but the difference is that here the concept of $\theta $ will be discussed. See in the diagram below:

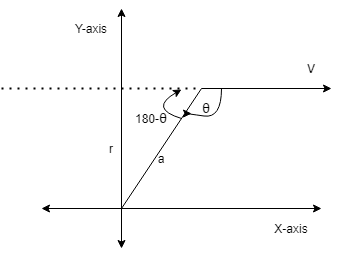
Here, $r$ is the perpendicular distance and $a$ is the distance covered by a body before going parallel to the x-axis and v is the velocity. All are in the X-Y plane.
Now, the angular momentum is denoted by $\mathop L\limits^ \to $ and formula for it is $\mathop L\limits^ \to $ =$\mathop r\limits^ \to \times \mathop p\limits^ \to $
where, $\mathop r\limits^ \to $ is the perpendicular distance between the path of the particle and x-axis, and $\mathop p\limits^ \to $ is the linear momentum of the particle and $\mathop p\limits^ \to $ =$m \times \mathop v\limits^ \to $ where m is the mass and v is the velocity
From the above diagram we can state that Angular momentum ($\mathop L\limits^ \to $) = (a) × ($m\mathop v\limits^ \to $ )
Cross product gives $\sin \theta $ so, ($\mathop L\limits^ \to $) = (a) ($m\mathop v\limits^ \to $ ) $\sin \theta $……… (1)
$\therefore $ $\sin \theta $=$\dfrac{{perpendicular}}{{hypotenuse}}$ and $\sin (180 - \theta ) \Rightarrow \sin \theta $
So, $\sin (180 - \theta )$ or $\sin \theta $=$\dfrac{r}{a}$ …….. (2)
Or it can also be written as r=$a\sin \theta $ …… (3)
Putting equation (3) in equation (1) we get, L=mvr
We have velocity, mass, and perpendicular distance all is constant. So angular momentum $\mathop L\limits^ \to $ will be constant.
Students usually make mistakes in understanding linear and angular momentum. Linear momentum is the inertia of translational motion whereas angular momentum is the inertia of rotational motion.
Momentum is denoted by p stated above and it is the product of mass and velocity of the object. In mathematical terms it is written as $\mathop p\limits^ \to $ =$m \times \mathop v\limits^ \to $ and it is always conserved so angular momentum will also be conserved.
Its S.I unit is $kg{m^2}$ ${s^{ - 1}}$.