Question

A (4,2), B (6,8) and C (8,4) are the vertices of triangle ABC. Write down the equation of the median of the triangle through A.

Answer 1

Hint: Median passing through A will pass through the midpoint of BC. Hence find the midpoint of BC and hence find the equation of the median using the two-point form of the equation of a line. Alternatively, we have a median that always passes through the centroid of the triangle. Hence find the coordinates of centroid and hence the equation of the line using the two-point form of the equation of a line.

Complete step-by-step answer:

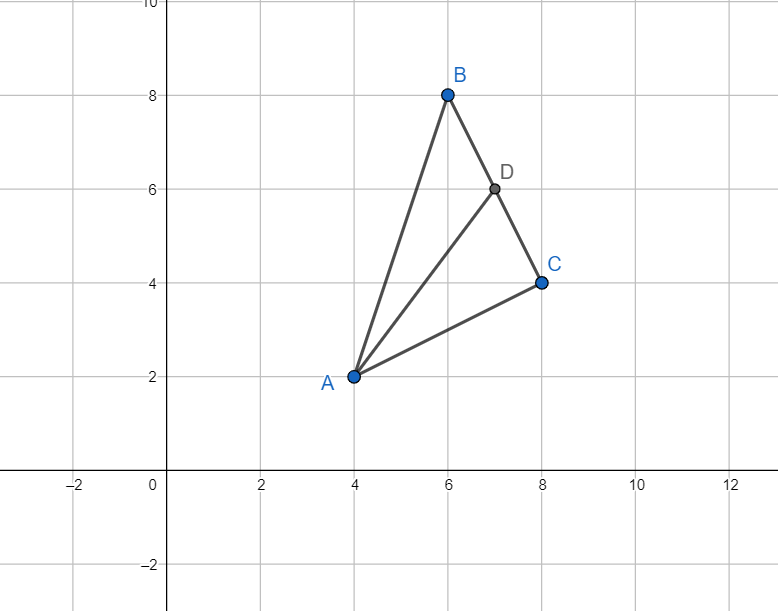
We know that the coordinates of the midpoint of $\text{A}\left( {{x}_{1}},{{y}_{1}} \right)$ and $\text{B}\left( {{x}_{2}},{{y}_{2}} \right)$ are given by $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Here ${{x}_{1}}=6,{{x}_{2}}=8,{{y}_{1}}=8$ and ${{y}_{2}}=4$.
Using the above formula, we get
Coordinates of D are given by $\left( \dfrac{6+8}{2},\dfrac{8+4}{2} \right)=\left( 7,6 \right)$
We know that equation of the line passing through $\text{A}\left( {{x}_{1}},{{y}_{1}} \right)$ and $\text{B}\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
$y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$
Hence the equation of the line passing through A (4,2) and D (7,6) is given by:
Here ${{x}_{1}}=4,{{x}_{2}}=7,{{y}_{1}}=2$ and ${{y}_{2}}=6$
Using the above formula we have the equation of the line is given by
$\begin{align}
  & y-2=\dfrac{6-2}{7-4}\left( x-4 \right) \\
 & \Rightarrow y-2=\dfrac{4}{3}\left( x-4 \right) \\
 & \Rightarrow 3y-6=4x-16 \\
 & \Rightarrow 3y=4x-10 \\
\end{align}$
Hence the equation of median of triangle ABC passing through A is given by 3y =4x-10.

Note: Alternate solution:
Coordintes of centroid of triangle ABC with $\text{A}\equiv \left( {{x}_{1}},{{y}_{1}} \right),\text{B}\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $\text{C}\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ are given by $\text{G}\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
Hence the coordinates of centroid of triangles ABC are given by $\left( \dfrac{6+8+4}{3},\dfrac{2+8+4}{3} \right)=\left( 6,\dfrac{14}{3} \right)$
Hence the equation of the line is given by
$\begin{align}
  & y-2=\dfrac{\dfrac{14}{3}-2}{6-4}\left( x-4 \right) \\
 & \Rightarrow y-2=\dfrac{8}{6}\left( x-4 \right) \\
 & \Rightarrow 3y-6=4x-16 \\
 & \Rightarrow 3y=4x-10 \\
\end{align}$
Hence the equation of median of triangle ABC passing through A is given by 3y =4x-10.