Question

A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.

Answer 1

Hint: In the above question, to find the area of the path we have to find the area of a park ABCD then we will add the width of path that is 3 m twice to find the length of PQ, in the same way we will find the width of QR by adding 3 m twice. We will find the area of PQRS. Then we will subtract the area of PQRS and the area of ABCD, we will get the area of the path.

Complete step-by-step answer:
Given,
Width of path running outside = 3 m
Length of rectangular park = 125 m
Breadth of rectangular park = 65 m

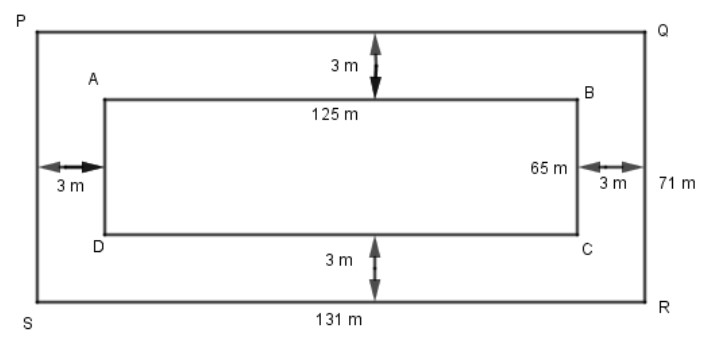
Area of rectangular park ABCD = length X breadth
$ = 125 \times 65 = 8,125{m^2}$.
Now, length of PQ = 125 + 3 + 3 = 131 m
Breadth of QR = 65 + 3 + 3 =71 m
$\text{Area of PQRS} = \text{length} \times \text{breadth}$
$ = 131 \times 71 = 9,301{m^2}$
Thus, the area of a path = Area of PQRS – Area of ABCD
$ = 9,301 - 8,125 = 1176{m^2}$.
Hence, the area of the path is $1176{m^2}$.

So, the correct answer is “Option A”.
Additional Information:

Note:Here you may notice that we have added 3 m twice to the length as well as breadth because (3m + 3m) is to cover both the sides of the length and breadth. First 3 m is for right side of the length of a rectangular park and second 3 m is for left side of the length of a rectangular park.Students should remember the formulas of area and perimeter of rectangle for solving these types of questions.