Questions & Answers
Question
Answers
Related Questions
A 25m long ladder is placed against a vertical wall such that the foot of the ladder is 7m from the feet of the wall. If the top of the ladder slides down by 4m by how much distance will the foot of the ladder slide ?
Answer
![Verified]()
Verified
Verified
Hint:Here we will find the height of the wall at which the ladder placed initially using the given length and horizontal distance. With the height we will find the height of the wall after sliding and with the help of the length of the ladder we will find the slided foot distance. Throughout the problem we will use the Pythagoras theorem.
Formula used: Pythagoras theorem
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicula{r^2}\; + {\rm{ }}Bas{e^2}\;\]
Complete step-by-step answer:
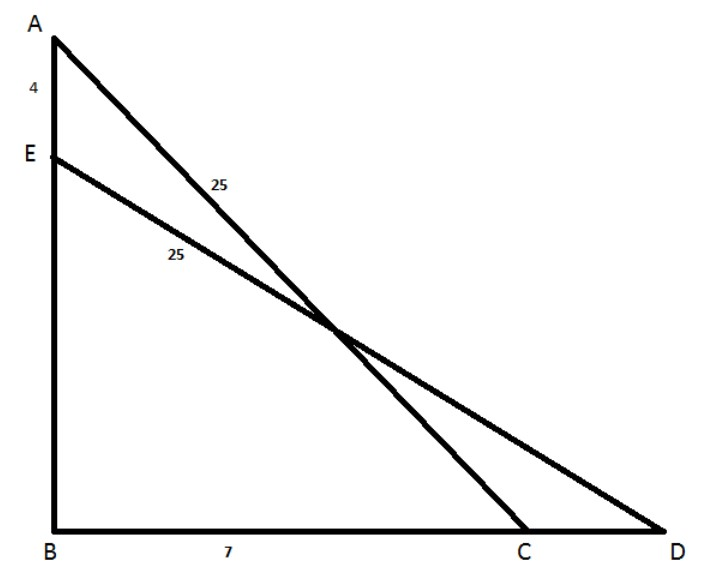
Here, it is given that length of the ladder = 25 m
That is from the diagram we have \[AC = ED = 25\]
Also given that the distance between the wall and the foot of the ladder is 7m.
That is \[CB = {\rm{ }}7\]
Here it is also given that the ladder slides 4m in the wall.
That is \[AE = 4\]
Before sliding, the situation is represented by a right triangle with hypotenuse 25, and base 7,
Using Pythagoras theorem we have,
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicula{r^2}\; + {\rm{ }}Bas{e^2}\;\]
We have to find the length of the wall, which is nothing but the perpendicular in the triangle.
\[{\rm{ }}Perpendicula{r^2}\; = Hypotenus{e^2} - {\rm{ }}Bas{e^2}\;\]
On comparing with the triangle we get,
\[A{B^2} = A{C^2} - C{B^2}\]
By substituting the values known we get,
\[A{B^2} = {25^2} - {7^2}\]
Let us square the terms in the right hand side we get,
\[A{B^2} = 625 - 49\]
By solving and taking square root on both the sides, we get
\[AB = \sqrt {576} \]
\[AB = 24{\rm{ }}m\]
Hence, the vertical arm that is the height of the wall is 24 m.
After sliding, the situation is represented by a right triangle with hypotenuse 25, and vertical arm has been slide 4 m then the vertical arm is of length \[24 - 4 = 20\]m,
Using Pythagoras theorem in this triangle, we get
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicular{r^2}\; + {\rm{ }}Bas{e^2}\;\]
We have to find the distance between the wall and foot of the ladder after sliding, that is we have to find the base of the triangle.
\[{\rm{ }}Bas{e^2}\;\; = Hypotenuse{e^2} - {\rm{ }}Perpendicula{r^2}\]
On comparing with the triangle we get,
\[D{B^2} = D{E^2} - E{B^2}\]
By substituting the known values we get
\[D{B^2} = {25^2} - {20^2}\]
Let us square and solve right hand side of the equation, we get,
\[D{B^2} = 625 - 400 = 225\]
By taking square root on both the sides, we get
\[DB = \sqrt {225} \]
\[DB = 15{\rm{ }}m\]
So that the distance between foot of ladder and wall is \[15{\rm{ }}m\]
To find the distance changed in the ladder foot is \[15 - 7 = 8{\rm{ }}m\]
Hence, the distance from the foot of the ladder slide is 8 m
Additional Information:Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle \[{90^ \circ }\].
Note:We can come to a conclusion that when a ladder is sliding in the height then the distance on the foot of the ladder increases. While sliding in the height we should subtract the initial height and the slided height.
Formula used: Pythagoras theorem
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicula{r^2}\; + {\rm{ }}Bas{e^2}\;\]
Complete step-by-step answer:
Here, it is given that length of the ladder = 25 m
That is from the diagram we have \[AC = ED = 25\]
Also given that the distance between the wall and the foot of the ladder is 7m.
That is \[CB = {\rm{ }}7\]
Here it is also given that the ladder slides 4m in the wall.
That is \[AE = 4\]
Before sliding, the situation is represented by a right triangle with hypotenuse 25, and base 7,
Using Pythagoras theorem we have,
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicula{r^2}\; + {\rm{ }}Bas{e^2}\;\]
We have to find the length of the wall, which is nothing but the perpendicular in the triangle.
\[{\rm{ }}Perpendicula{r^2}\; = Hypotenus{e^2} - {\rm{ }}Bas{e^2}\;\]
On comparing with the triangle we get,
\[A{B^2} = A{C^2} - C{B^2}\]
By substituting the values known we get,
\[A{B^2} = {25^2} - {7^2}\]
Let us square the terms in the right hand side we get,
\[A{B^2} = 625 - 49\]
By solving and taking square root on both the sides, we get
\[AB = \sqrt {576} \]
\[AB = 24{\rm{ }}m\]
Hence, the vertical arm that is the height of the wall is 24 m.
After sliding, the situation is represented by a right triangle with hypotenuse 25, and vertical arm has been slide 4 m then the vertical arm is of length \[24 - 4 = 20\]m,
Using Pythagoras theorem in this triangle, we get
\[Hypotenus{e^2}\; = {\rm{ }}Perpendicular{r^2}\; + {\rm{ }}Bas{e^2}\;\]
We have to find the distance between the wall and foot of the ladder after sliding, that is we have to find the base of the triangle.
\[{\rm{ }}Bas{e^2}\;\; = Hypotenuse{e^2} - {\rm{ }}Perpendicula{r^2}\]
On comparing with the triangle we get,
\[D{B^2} = D{E^2} - E{B^2}\]
By substituting the known values we get
\[D{B^2} = {25^2} - {20^2}\]
Let us square and solve right hand side of the equation, we get,
\[D{B^2} = 625 - 400 = 225\]
By taking square root on both the sides, we get
\[DB = \sqrt {225} \]
\[DB = 15{\rm{ }}m\]
So that the distance between foot of ladder and wall is \[15{\rm{ }}m\]
To find the distance changed in the ladder foot is \[15 - 7 = 8{\rm{ }}m\]
Hence, the distance from the foot of the ladder slide is 8 m
Additional Information:Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle \[{90^ \circ }\].
Note:We can come to a conclusion that when a ladder is sliding in the height then the distance on the foot of the ladder increases. While sliding in the height we should subtract the initial height and the slided height.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
