
A 1.5m tall boy is standing at some distance from a 30m tall building. The angle of elevation from his eyes to the top of the building increases from $30{}^\circ $to $60{}^\circ $as he walks towards the building. Find the distance he walked towards the building.
Answer
606.6k+ views
Hint: Draw a neat diagram representing boy and building with angle of elevations and height of boy and building both. Now, use trigonometry functions in triangles formed to get the answer.
Complete step-by-step answer:
Here, we need to draw a suitable diagram with the help of given information.
It is given that the boy is of height 1.5m and he walks towards a building of length 30m from ground and angle of elevation from his eyes to the top of the building is increasing from $30{}^\circ $ to $60{}^\circ $.
Hence, diagram can be given as
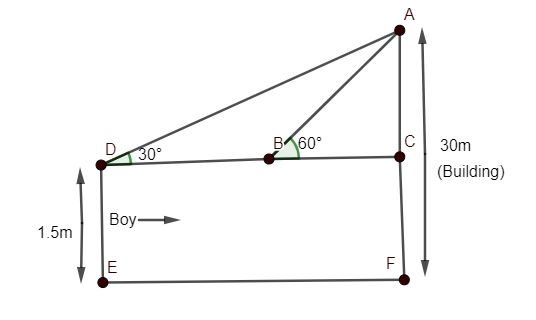
As we need to determine the distance walked by boy towards the building i.e. distance DB from the diagram.
Now, DE=CF=1.5m (as per the diagram)
Hence, length AC can be calculated by
AC = AF-CF i.e.,
AC = 30-1.5
So, AC=28.5m
In triangle ABC, let us evaluate$\tan 60{}^\circ $,
As we know
$\tan \theta =\dfrac{Perpendicular}{base}$
Hence, $\tan 60{}^\circ $ in $\Delta ABC$ can be given as
$\tan 60{}^\circ =\dfrac{AC}{BC}=\dfrac{28.5}{BC}$
We know the value of $\tan 60{}^\circ $ is $\sqrt{3}$.
Hence, we can get BC from the above equation as
$\sqrt{3}=\dfrac{28.5}{BC}$
or$BC=\dfrac{28.5}{\sqrt{3}}\ldots \ldots (1)$
Now, similarly, take $\tan 30{}^\circ $ from $\Delta ADC$; hence, we get
$\tan 30{}^\circ =\dfrac{AC}{CD}\ldots \ldots (2)$
We can observe from the side CD such that it can be written as a summation of two sides BD and BC.
So, CD=BD+BC
Now, from equation (1), we have already calculated the value of BC as $\dfrac{28.5}{\sqrt{3}}$.
So,
$CD=BD+\dfrac{28.5}{\sqrt{3}}$$\ldots \ldots (3)$
Now, putting value of CD in terms of BC in equation (2), we get
$\tan 30{}^\circ =\dfrac{AC}{\left( BD+\dfrac{28.5}{\sqrt{3}} \right)}$
Now we know the value of $\tan 30{}^\circ $ can be given as \[\dfrac{1}{\sqrt{3}}\] and length AC is 28.5m.
Hence, we get
$\dfrac{1}{\sqrt{3}}=\dfrac{28.5}{\left( BD+\dfrac{28.5}{\sqrt{3}} \right)}$
On cross-multiplying the above equation, we get
$BD+\dfrac{28.5}{\sqrt{3}}=28.5\sqrt{3}$
Hence,
$BD=28.5\sqrt{3}-\dfrac{28.5}{\sqrt{3}}$
or
$BD=28.5\left( \sqrt{3}-\dfrac{1}{\sqrt{3}} \right)$
Hence, BC can be given as
$BD=28.5\left( \dfrac{3-1}{\sqrt{3}} \right)=\dfrac{28.5\times 2}{\sqrt{3}}$
Multiplying by $\sqrt{3}$ in numerator and denominator, we get
\[BD=\dfrac{28.5\times 2\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\dfrac{28.5\times 2\times \sqrt{3}}{3}\]
Or
$BD=9.5\times 2\times \sqrt{3}$
Now, we know the value of $\sqrt{3}$ is 1.7325.
Hence,
$BD=19\times 1.7325$
$BD=32.9175m\approx 33m$
Hence, the distance the boy walked towards the building is 33 metres.
Note: One can go wrong if he/she ignores the height of the boy. The length of AC is 30-1.5=28.5m. So, one can ignore height but which will give the wrong solution. As angle of elevation is measured from top of boy so, we cannot ignore the height of boy to get an accurate answer.
Using any other trigonometry functions except tan and cot will not solve the problem. So, please be careful with the information.
Complete step-by-step answer:
Here, we need to draw a suitable diagram with the help of given information.
It is given that the boy is of height 1.5m and he walks towards a building of length 30m from ground and angle of elevation from his eyes to the top of the building is increasing from $30{}^\circ $ to $60{}^\circ $.
Hence, diagram can be given as

As we need to determine the distance walked by boy towards the building i.e. distance DB from the diagram.
Now, DE=CF=1.5m (as per the diagram)
Hence, length AC can be calculated by
AC = AF-CF i.e.,
AC = 30-1.5
So, AC=28.5m
In triangle ABC, let us evaluate$\tan 60{}^\circ $,
As we know
$\tan \theta =\dfrac{Perpendicular}{base}$
Hence, $\tan 60{}^\circ $ in $\Delta ABC$ can be given as
$\tan 60{}^\circ =\dfrac{AC}{BC}=\dfrac{28.5}{BC}$
We know the value of $\tan 60{}^\circ $ is $\sqrt{3}$.
Hence, we can get BC from the above equation as
$\sqrt{3}=\dfrac{28.5}{BC}$
or$BC=\dfrac{28.5}{\sqrt{3}}\ldots \ldots (1)$
Now, similarly, take $\tan 30{}^\circ $ from $\Delta ADC$; hence, we get
$\tan 30{}^\circ =\dfrac{AC}{CD}\ldots \ldots (2)$
We can observe from the side CD such that it can be written as a summation of two sides BD and BC.
So, CD=BD+BC
Now, from equation (1), we have already calculated the value of BC as $\dfrac{28.5}{\sqrt{3}}$.
So,
$CD=BD+\dfrac{28.5}{\sqrt{3}}$$\ldots \ldots (3)$
Now, putting value of CD in terms of BC in equation (2), we get
$\tan 30{}^\circ =\dfrac{AC}{\left( BD+\dfrac{28.5}{\sqrt{3}} \right)}$
Now we know the value of $\tan 30{}^\circ $ can be given as \[\dfrac{1}{\sqrt{3}}\] and length AC is 28.5m.
Hence, we get
$\dfrac{1}{\sqrt{3}}=\dfrac{28.5}{\left( BD+\dfrac{28.5}{\sqrt{3}} \right)}$
On cross-multiplying the above equation, we get
$BD+\dfrac{28.5}{\sqrt{3}}=28.5\sqrt{3}$
Hence,
$BD=28.5\sqrt{3}-\dfrac{28.5}{\sqrt{3}}$
or
$BD=28.5\left( \sqrt{3}-\dfrac{1}{\sqrt{3}} \right)$
Hence, BC can be given as
$BD=28.5\left( \dfrac{3-1}{\sqrt{3}} \right)=\dfrac{28.5\times 2}{\sqrt{3}}$
Multiplying by $\sqrt{3}$ in numerator and denominator, we get
\[BD=\dfrac{28.5\times 2\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\dfrac{28.5\times 2\times \sqrt{3}}{3}\]
Or
$BD=9.5\times 2\times \sqrt{3}$
Now, we know the value of $\sqrt{3}$ is 1.7325.
Hence,
$BD=19\times 1.7325$
$BD=32.9175m\approx 33m$
Hence, the distance the boy walked towards the building is 33 metres.
Note: One can go wrong if he/she ignores the height of the boy. The length of AC is 30-1.5=28.5m. So, one can ignore height but which will give the wrong solution. As angle of elevation is measured from top of boy so, we cannot ignore the height of boy to get an accurate answer.
Using any other trigonometry functions except tan and cot will not solve the problem. So, please be careful with the information.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

What happens to glucose which enters nephron along class 10 biology CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




