NEET Chapter - The Solid State

In this chapter, we'll look at alternative particle configurations that can result in a variety of structures. The relationship between the nature of interactions within constituent particles and a variety of solid properties will also be investigated. It would also be explained how these qualities are affected by structural defects or by the presence of impurities in trace amounts.

This chapter is one of the easiest, most significant and scoring chapters for competitive tests like NEET, and mastering it will help you score well in the exams.

Important Topics of The Solid State:

• Amorphous Solid

• Difference Between Crystalline and Amorphous Solid

• Classification of Crystalline Solids

• Crystal Lattices and Unit Cell

• Unit Cell Packing Efficiency

• Imperfections or Defects in a Solid

Important Definitions of The Solid State

Solid-State

• Properties of Solids:  

The following are the characteristics of solids:

• They have fixed shape, mass and volume.

• The intermolecular force of attraction is strong.

• The intermolecular distance between the constituent particles of solids is short.

• They are rigid and incompressible.

• They have high density.

• Classification of Solids:

Solids are classified on the basis of the following properties

• On the basis of the arrangement of constituent particles and different properties:

• Amorphous Solids

• Crystalline Solids

• On the basis of bonding:

• Molecular Solids- They are further classified into polar, non-polar and  hydrogen-bonded.

• Ionic Solids

• Metallic Solids

• Covalent or network Solids

Amorphous and Crystalline Solids

Amorphous solids have constituent particles arranged in the crystal in an irregular pattern whereas in crystalline solids the constituents particles are arranged in a regular pattern. This leads to the difference in the properties of amorphous and crystalline solids.

Types of Crystalline  Solids on the Basis of Bonding

Graphite and Diamond:

Graphite and diamond are the covalent solids, but they are different in most of the properties as shown below:

Structure of Crystalline Solids

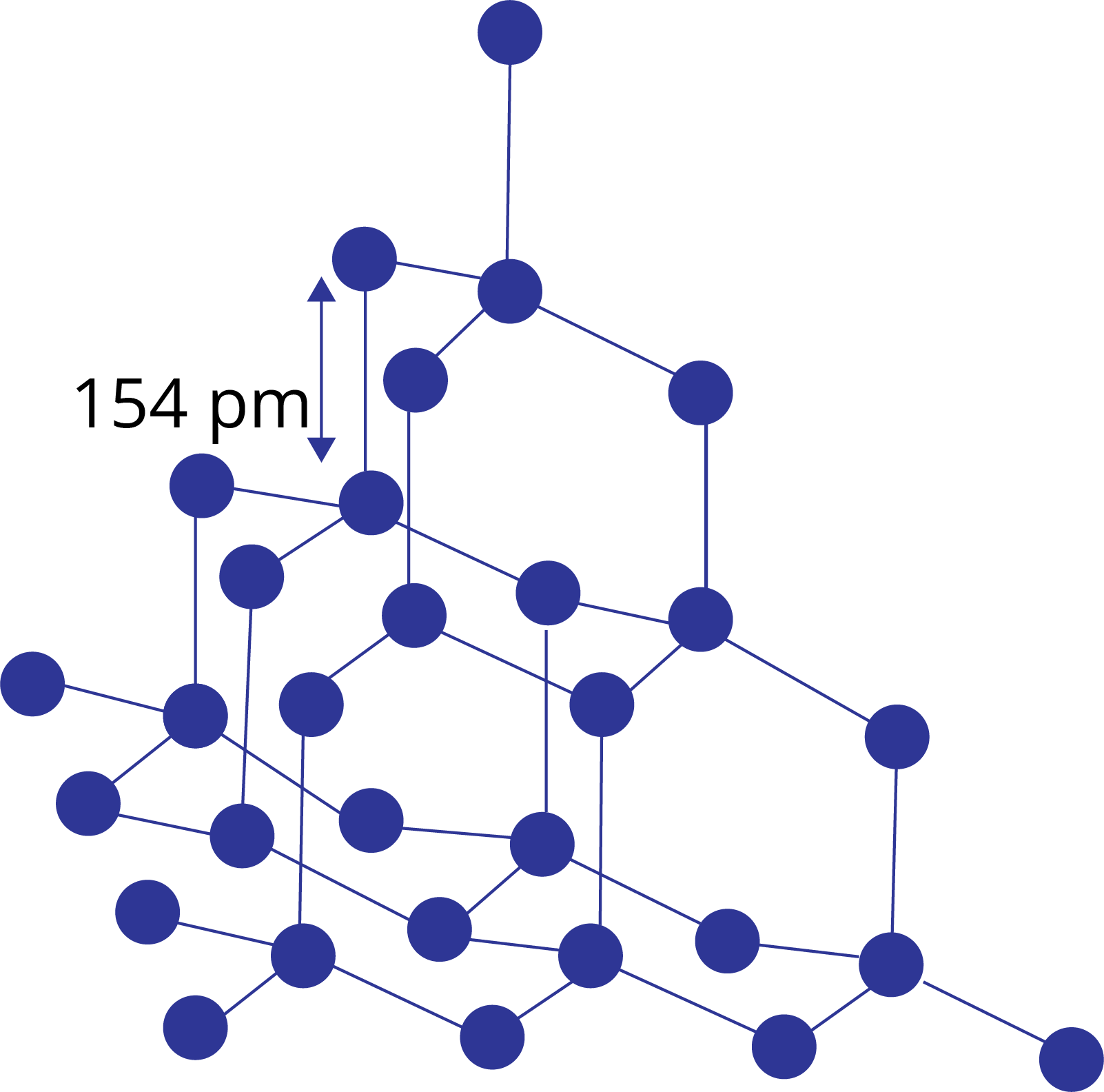
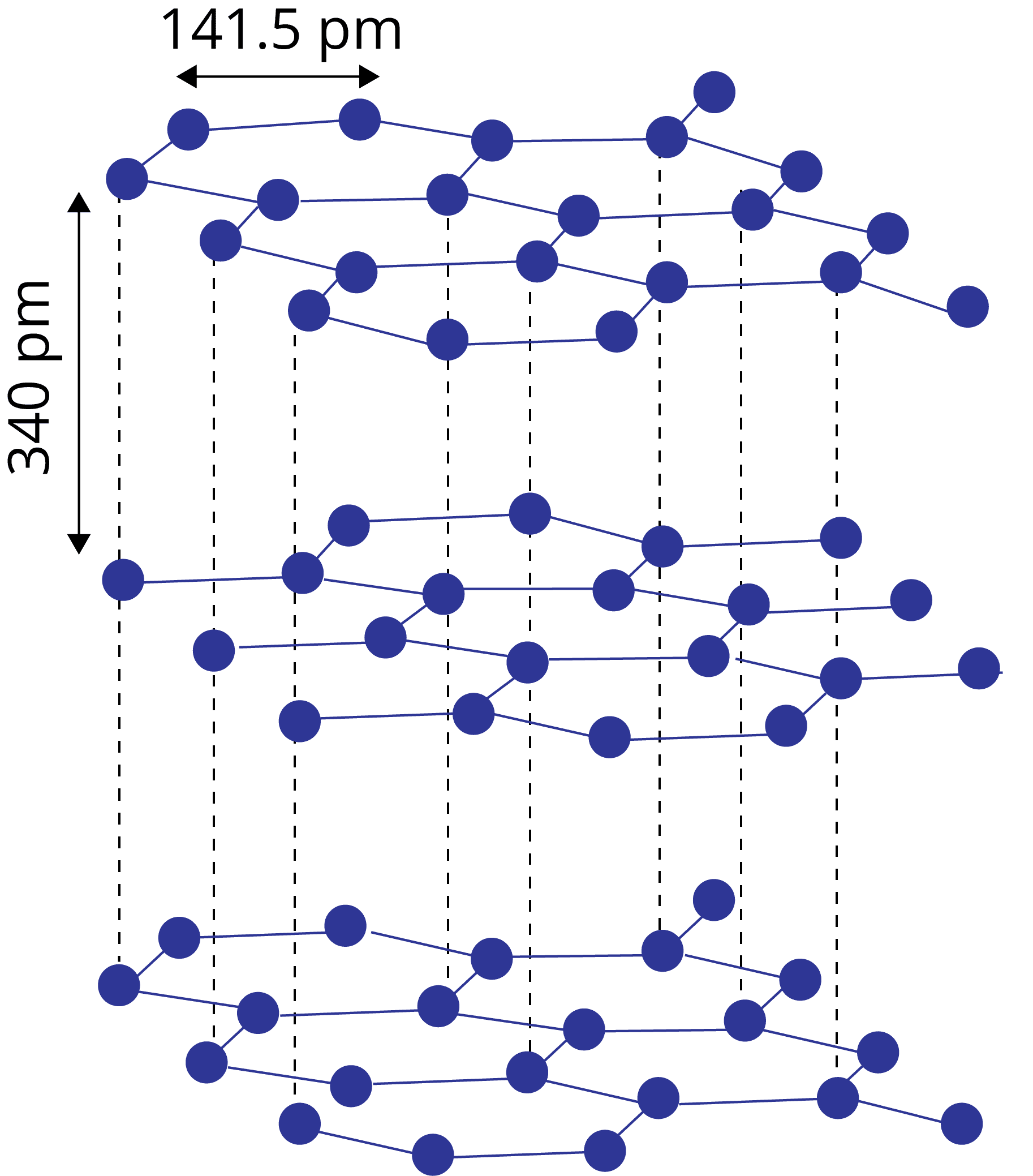
Crystal Lattice and Unit Cell:  The regular three-dimensional spatial arrangement of atoms, ions or molecules in the solids is known as the crystal lattice. 

The smallest component of a crystal lattice that is repeated in all directions to form the entire crystal lattice is referred to as a unit cell. 

In a unit cell, atoms of ions or molecules are represented by the sphere and the different types of the lattice is formed due to variation in the following parameters:

• Edge lengths: a,b,c

• Interfacial angles: α, β, γ

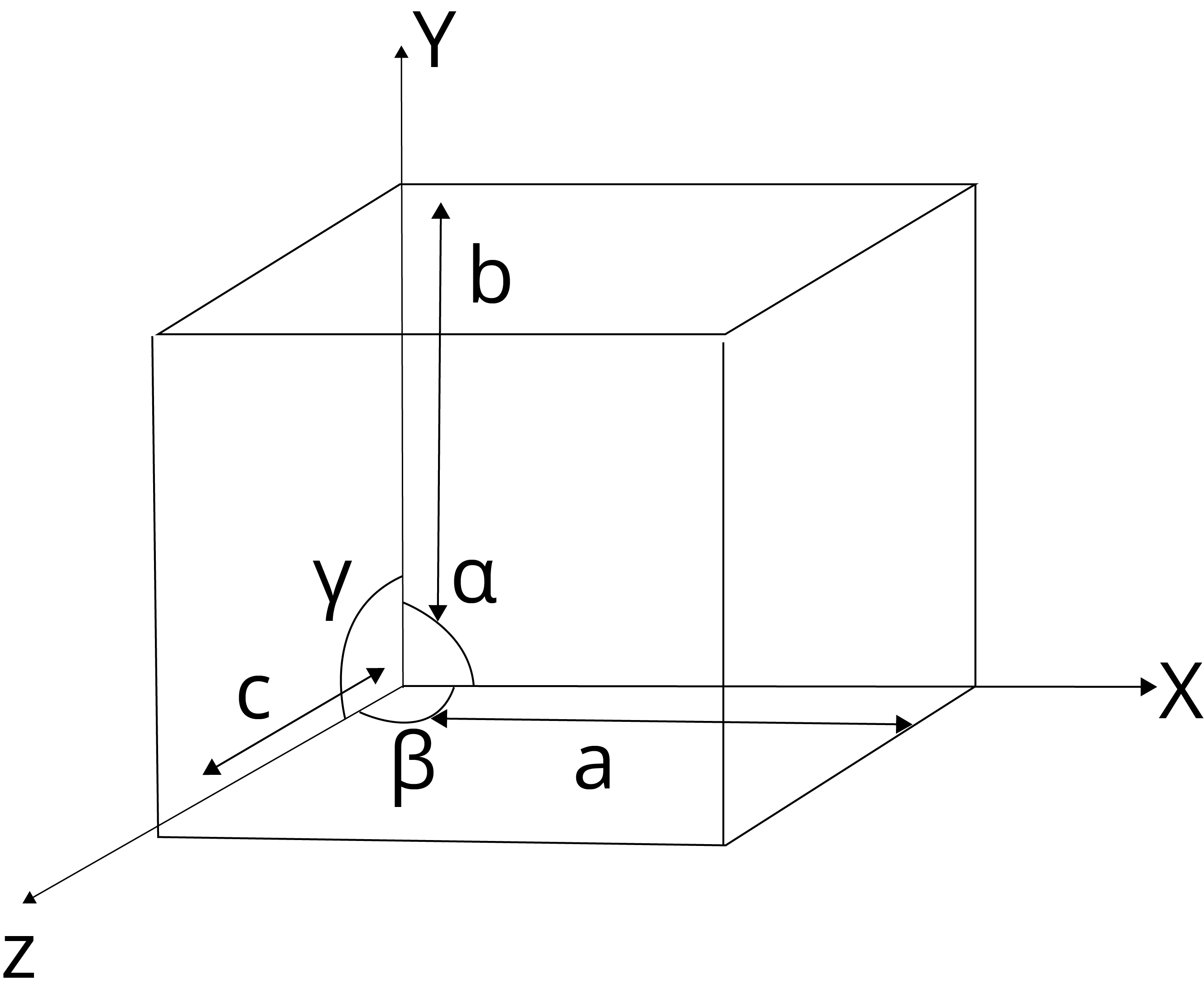
      Fig.: parameters of unit cell

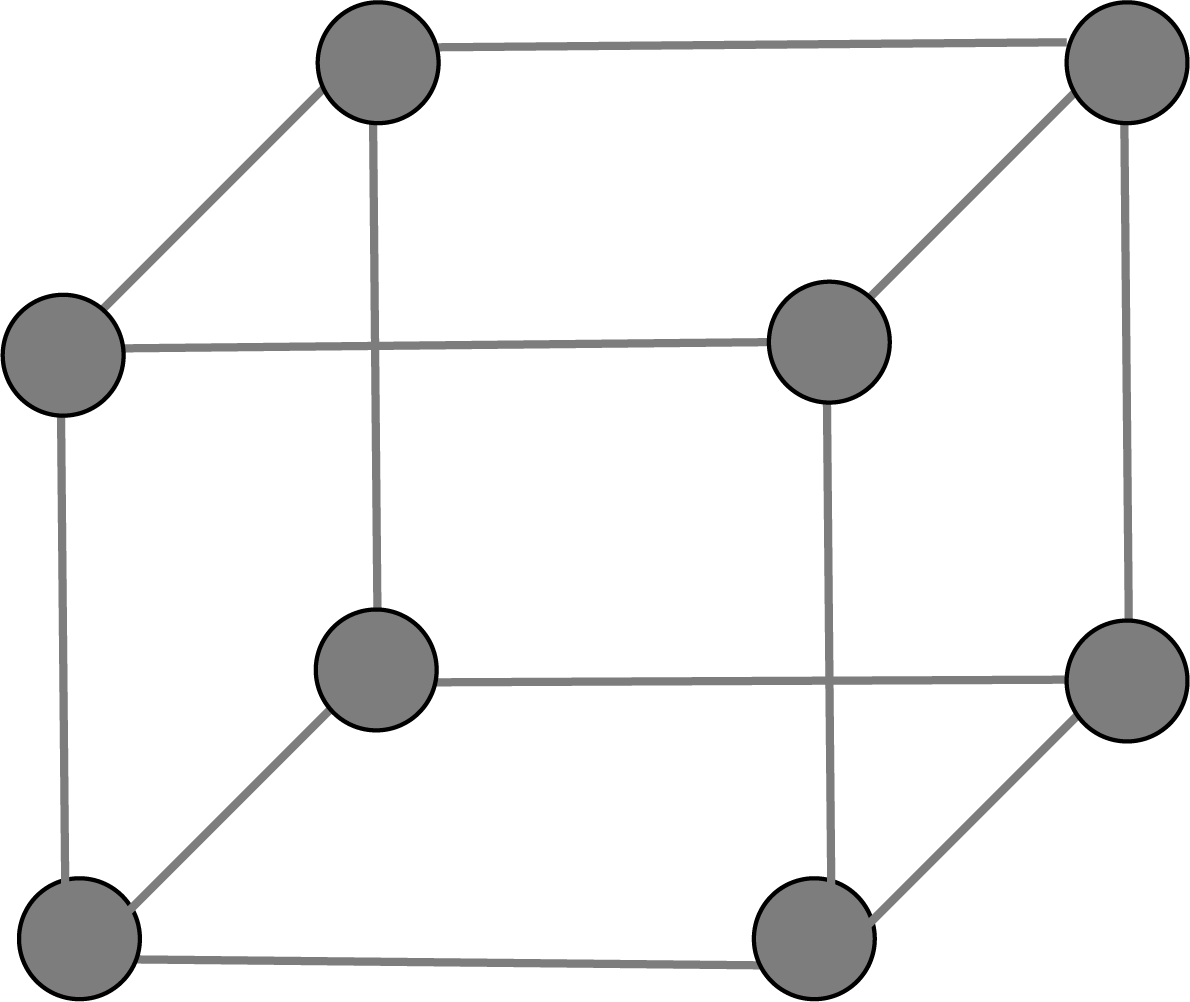
• Primitive Unit Cell:

There are generally 7 types of unit cells based on the variation in parameters of the unit cell in which the constituent atoms of ions or molecules present at the corner of the cell are known as primitive unit cells.

Table: 7 Primitive Unit Cells

• Centered  Unit Cell: A centered unit cell is one that comprises one or more constituent particles in positions other than the corners in addition to those at the corners. 

There are three types of centred unit cells:

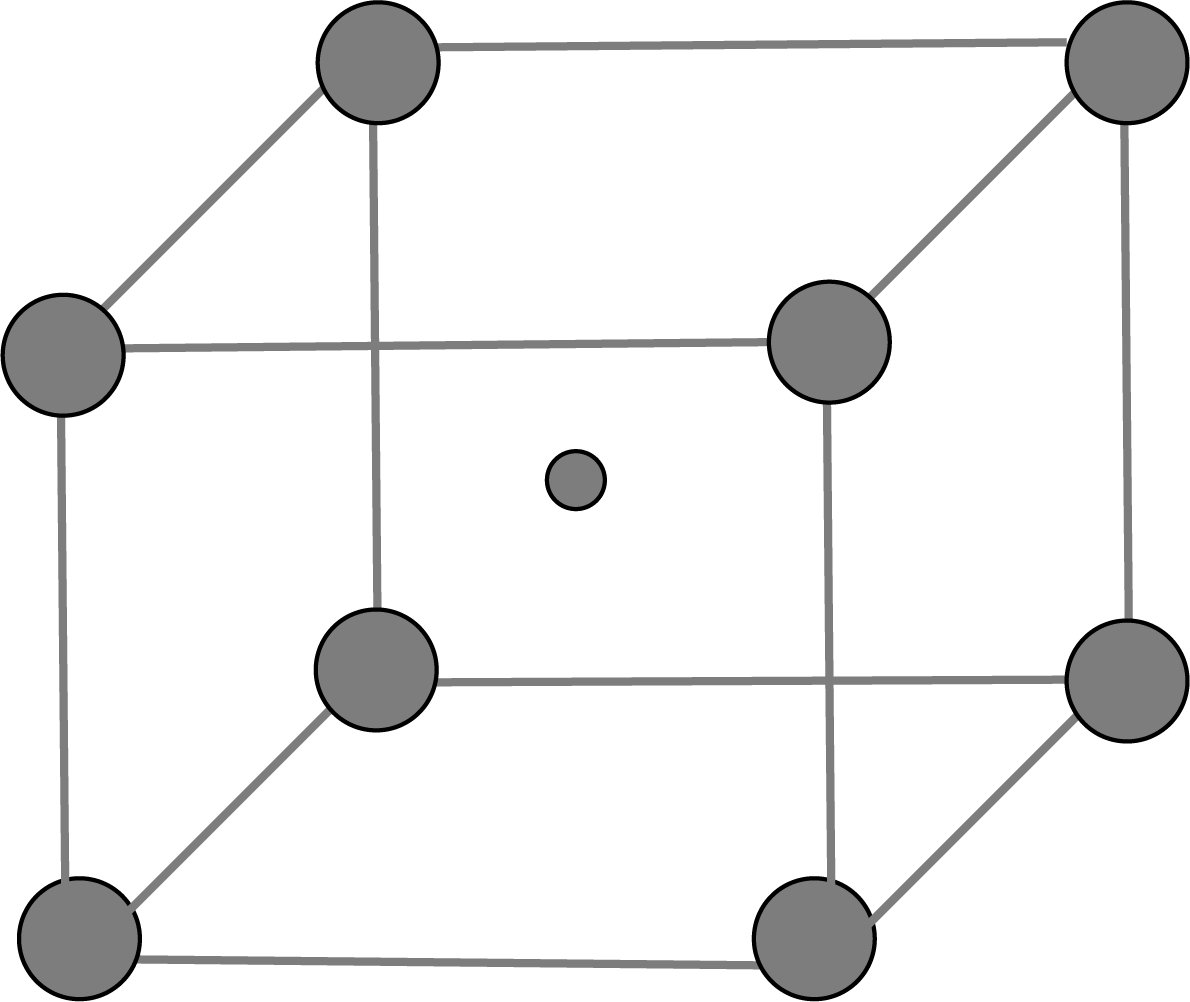
• Body-Centered Unit Cells: This type of unit cell contains one constituent(atom, ion or molecule) at the body centre in addition to those present at the corners. 

• Face-Centered Unit Cells: This type of unit cell contains one constituent(atom, ion or molecule) at the centre of each face in addition to those present at the corners.

• End-Centered Unit Cells: This type of unit cell contains one constituent(atom, ion or molecule) at the centre of any two opposite faces in addition to those present at the corners.

Contribution of spherical constituents are as follows:

• Corner:  ⅛ of number of constituent particles at the corner

• Body centre: 1

• Face centre: ⅓ of number of constituent particles at the faces

Density of Cubic Crystals

Density of cubic crystals is given by the formula:

Density,  ρ = $\dfrac{M \times Z}{a^{3}N_A}$

where M: Molar mass of solid

             Z:  Total number of atom in the unit cell

             A:  Edge length

             NA: Avogadro number

Close Packing in Solids

Suppose we have spheres of identical size that must be arranged in a single layer with the requirement that the spheres be in close contact with each other. There are two types of possible packing:

• Square packing

• Hexagonal packing

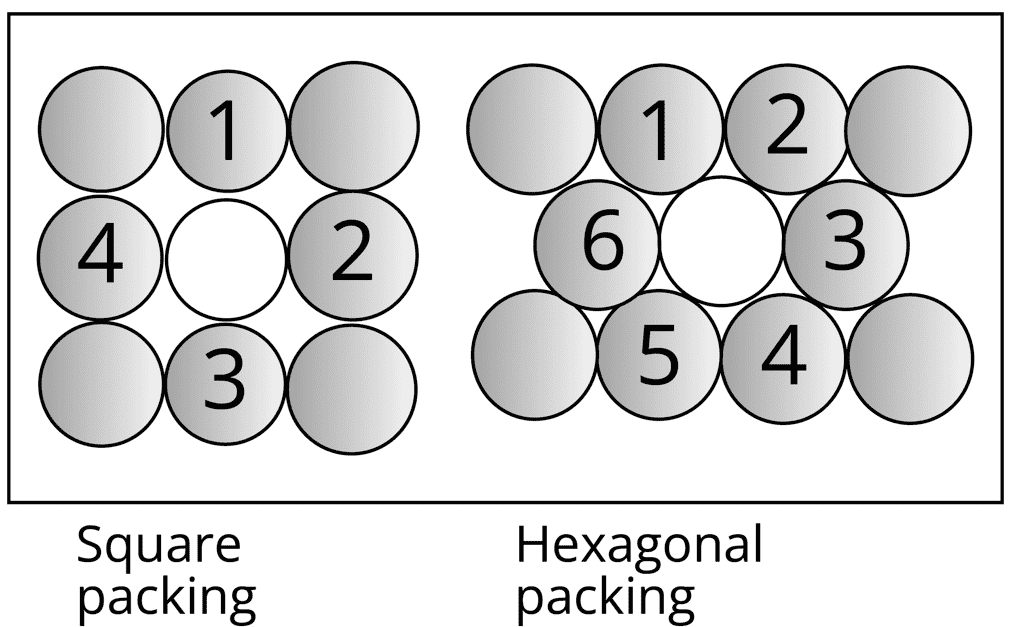
Hexagonal packing is more efficient:

• In hexagonal packing, the coordination number is 6, whereas, in square packing, the coordination number is 4. 

• In hexagonal packing square packing the size of the void is bigger than that of hexagonal packing. 

If we add another layer to the square packing, then there are the following possibilities:

• Simple Cubic Unit Cell: A comparable layer is placed just above the foundation layer, with the second layer's spheres coming just above the first layer's spheres, and the layers are repeated. The first layer is referred to as A, and the packing is of the AA... type, and the unit cell is a simple cubic unit cell.

• BCC Unit Cell: When the spheres of the second layer are positioned in the depressions of the first layer, we get the ABAB…… packing type and the unit cell is the BCC unit cell.
  
  

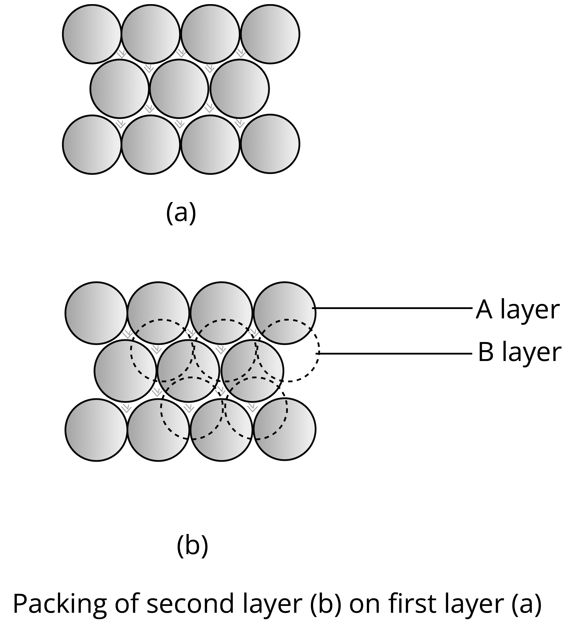
The types of arrangement of spheres in hexagonal packing in the voids are:

• When the second hexagonal layer is placed in the depressions of the first hexagonal layer A, two types of voids are formed.

• X type of voids are those which are hollow and through voids of layer A and layer B while Y type of voids are those voids of layer B which are exactly above spheres of layer A.

• If the sphere of the 2nd layer is placed on Y type void, then the 1st layer is repeated and ABABAB…. type hexagonal unit cell is obtained and the packing is hexagonal close packing(HCP). The efficiency of hexagonal close packing is 74%.
  
  

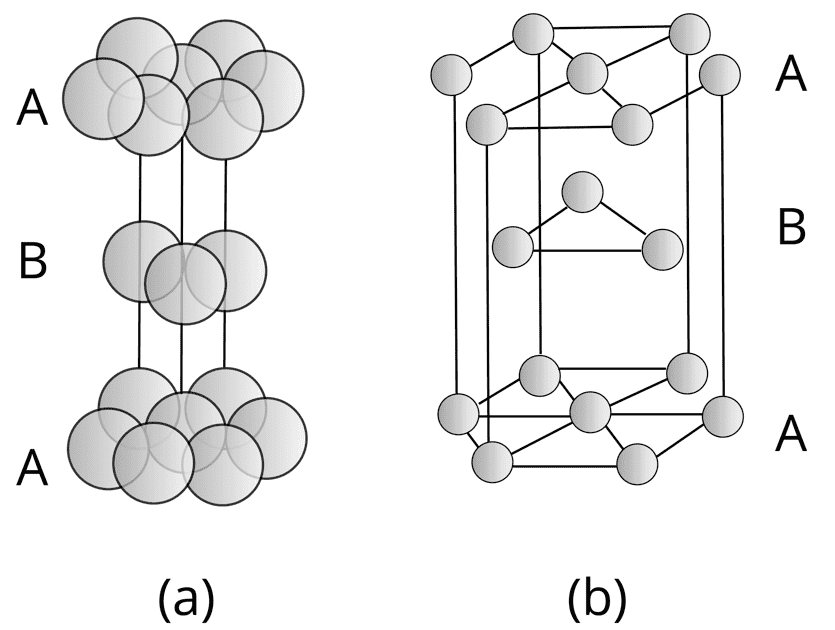
• When the 3rd layer is placed on X type of void, then a new layer C is obtained, and the packing is ABCABC…. Type. The unit cell for this type of arrangement is face-centred cubic (FCC) or cubic close packing(CCP). The efficiency of FCC or CCP is 74%.

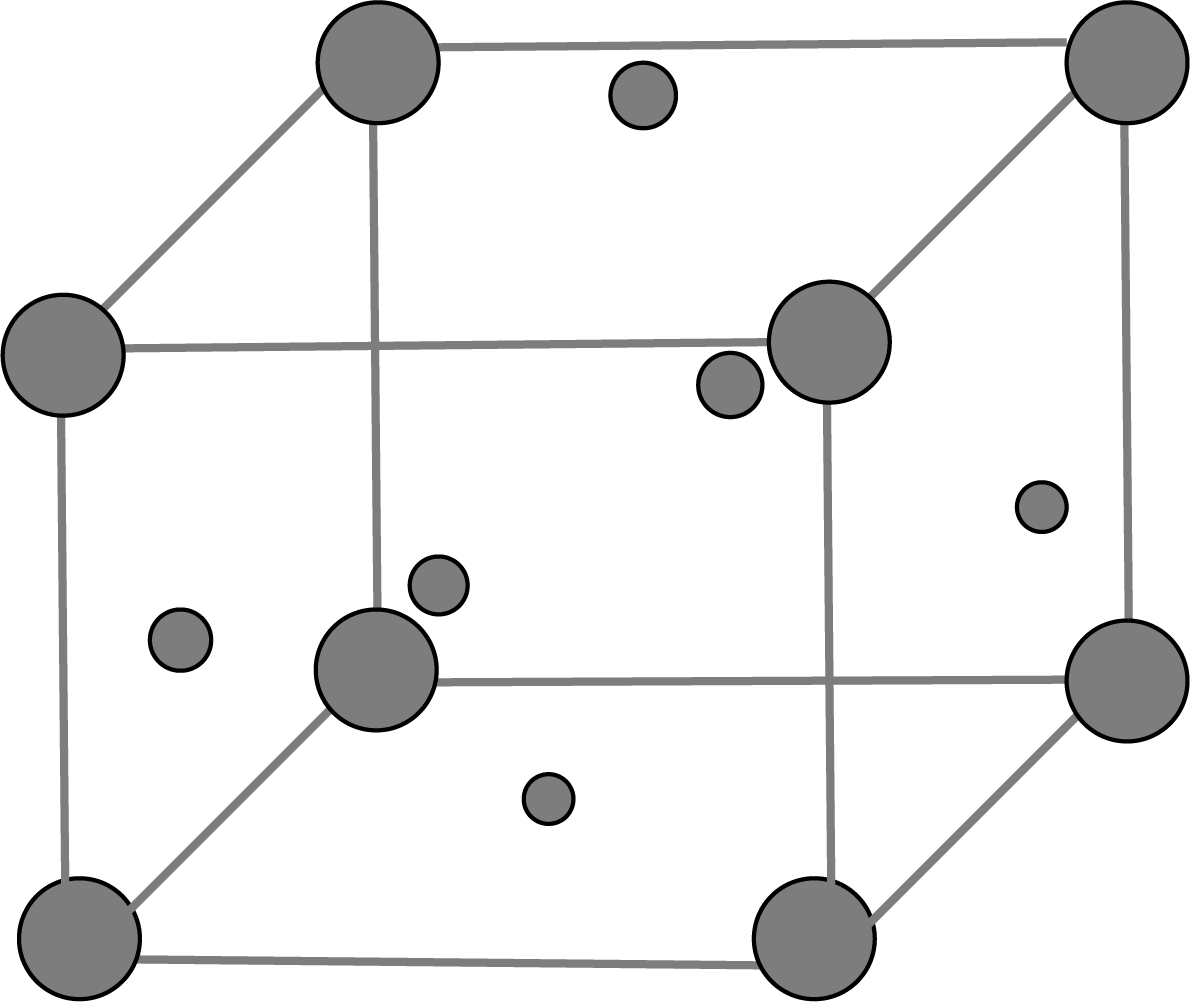
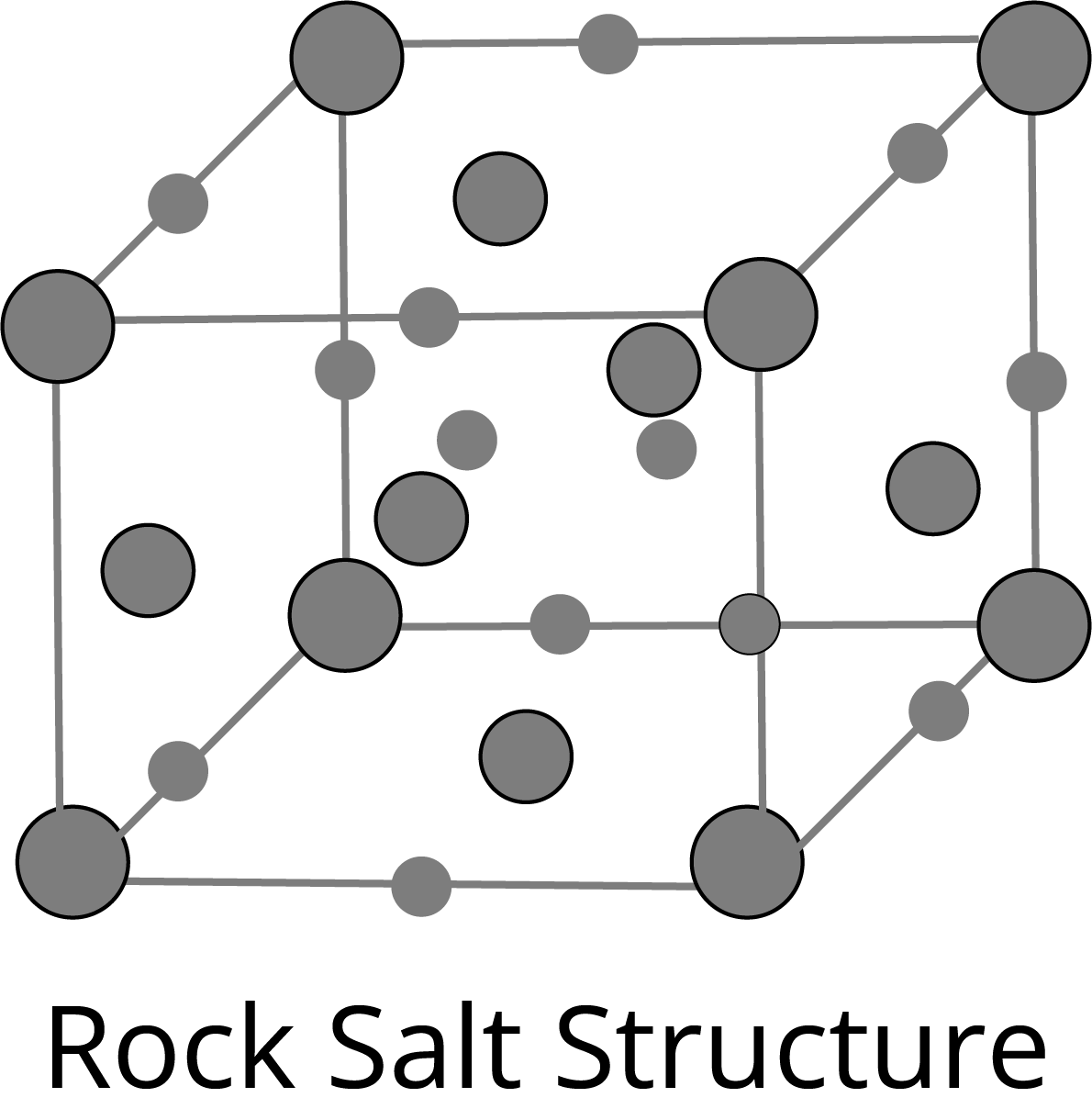
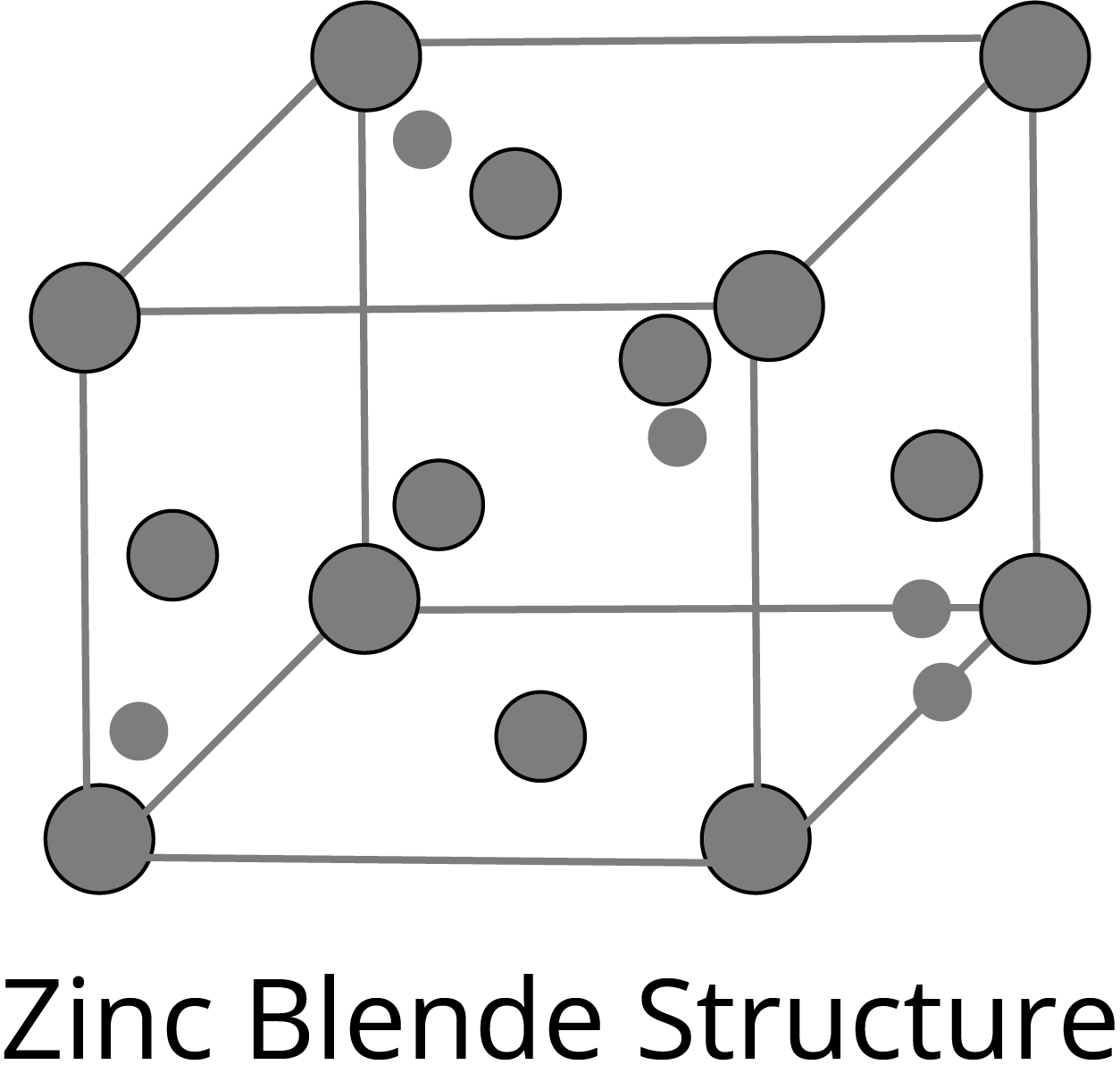
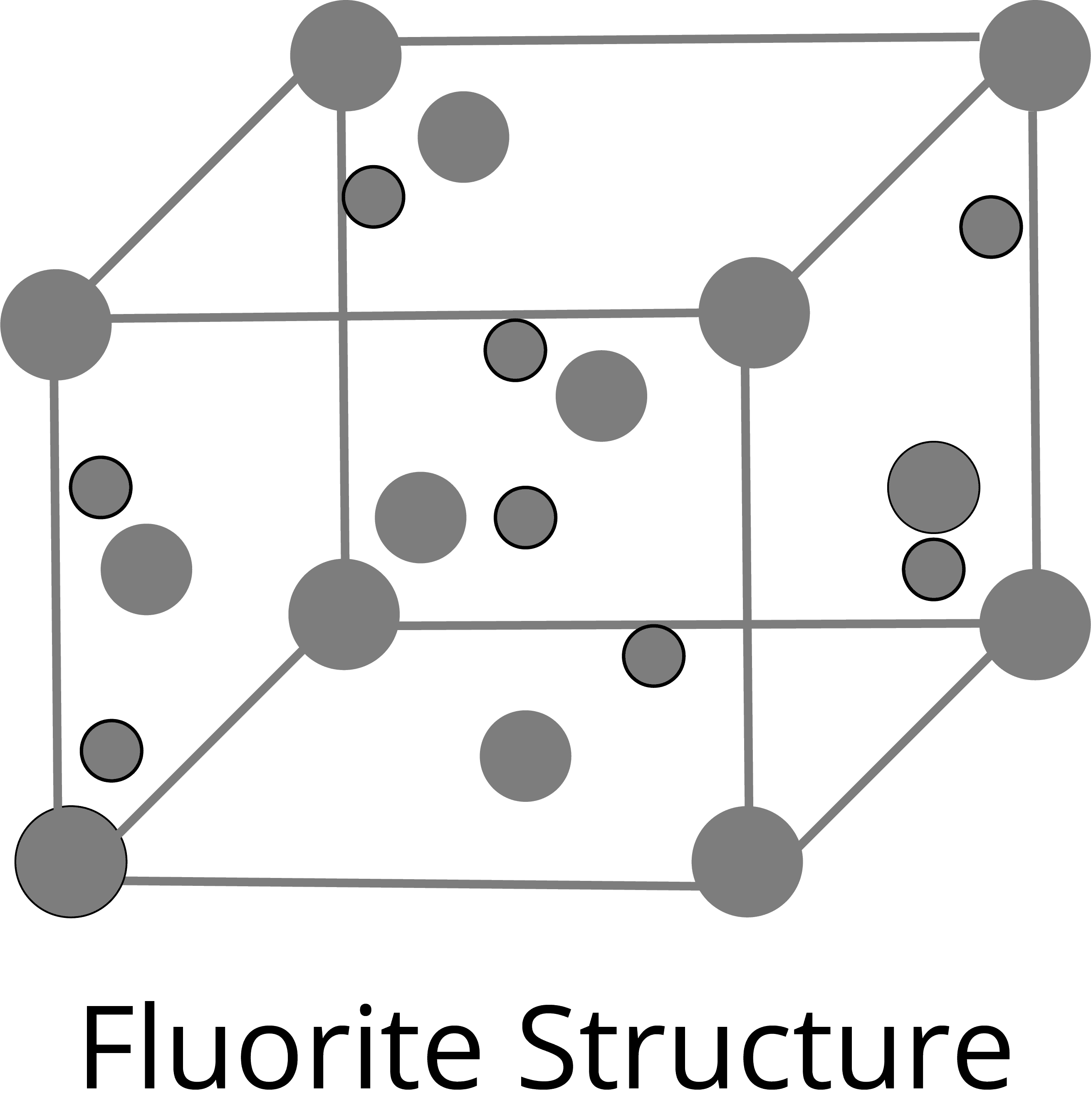
Classification of Ionic Structures

In the ionic structure, the ion of larger size occupies the main position whereas the smaller one occupies the void position. The size is decide by the radius ratio r+/r-

Based on the ratio range, there are five types of ionic structures:

• NaCl Type Structure:

• ZnS Type Structure:

• Fluorite Type Structure:

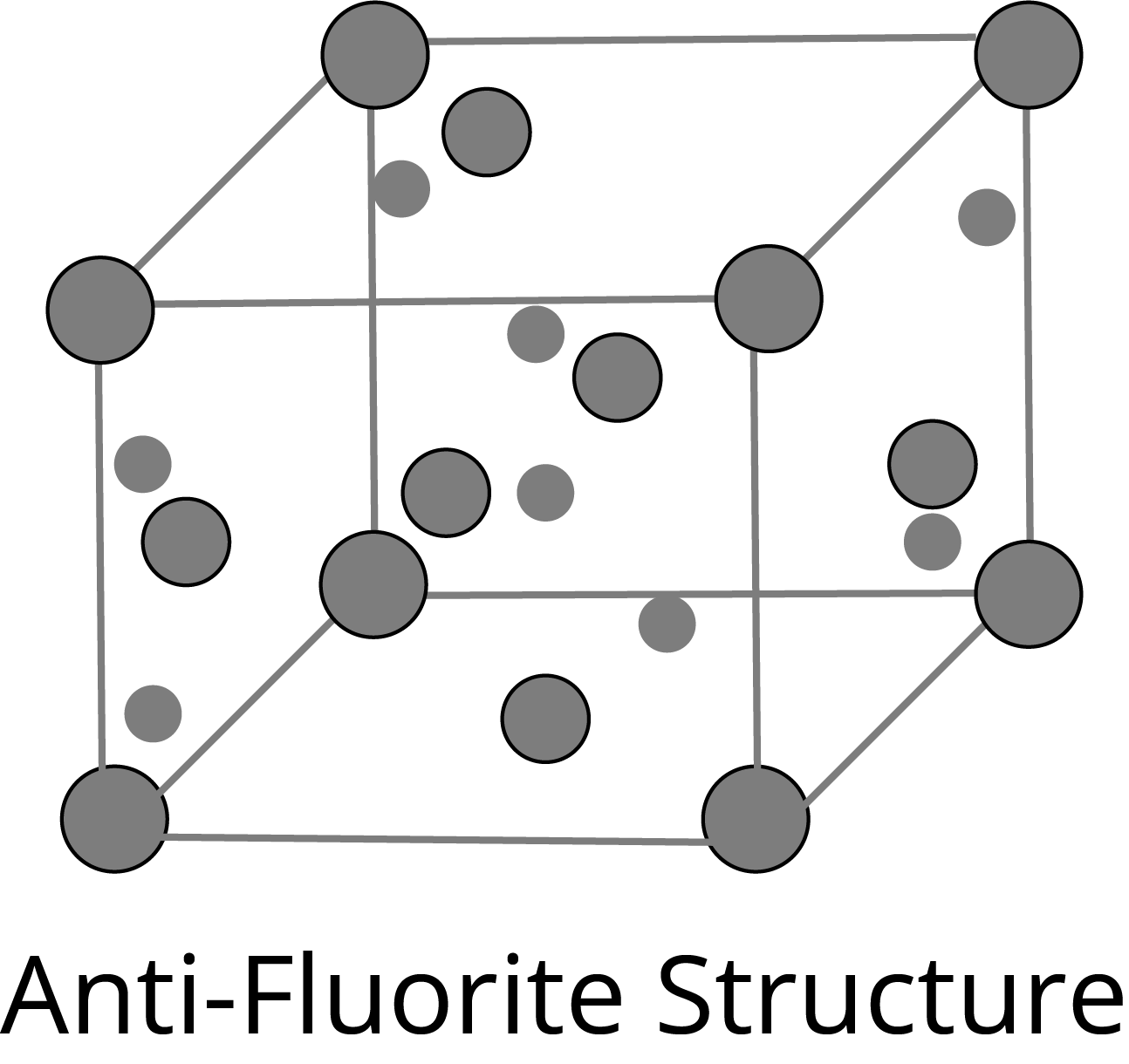
• Anti-fluorite Structure:

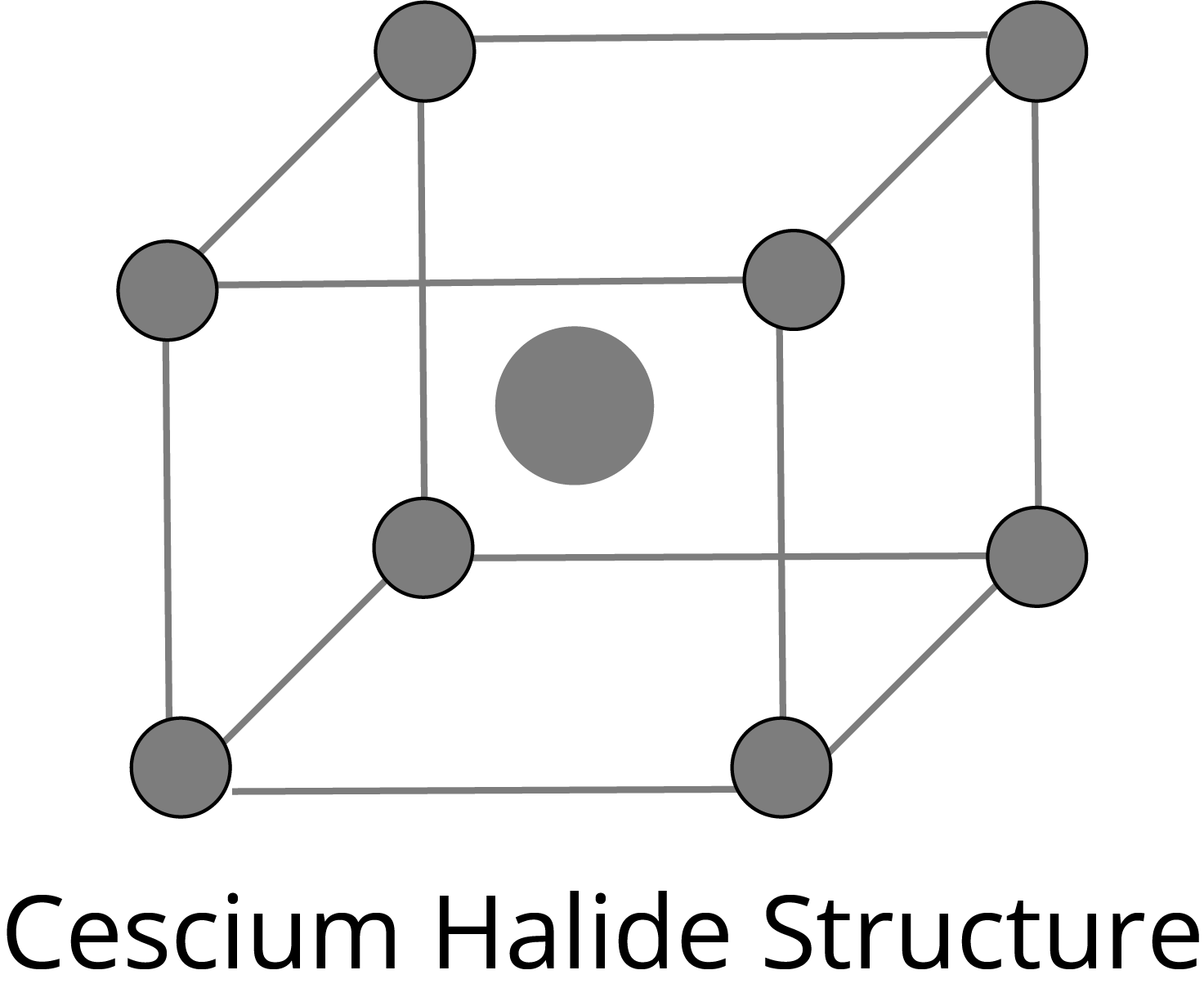
• CsCl Type Structure:

Imperfection or Defects in Solids:

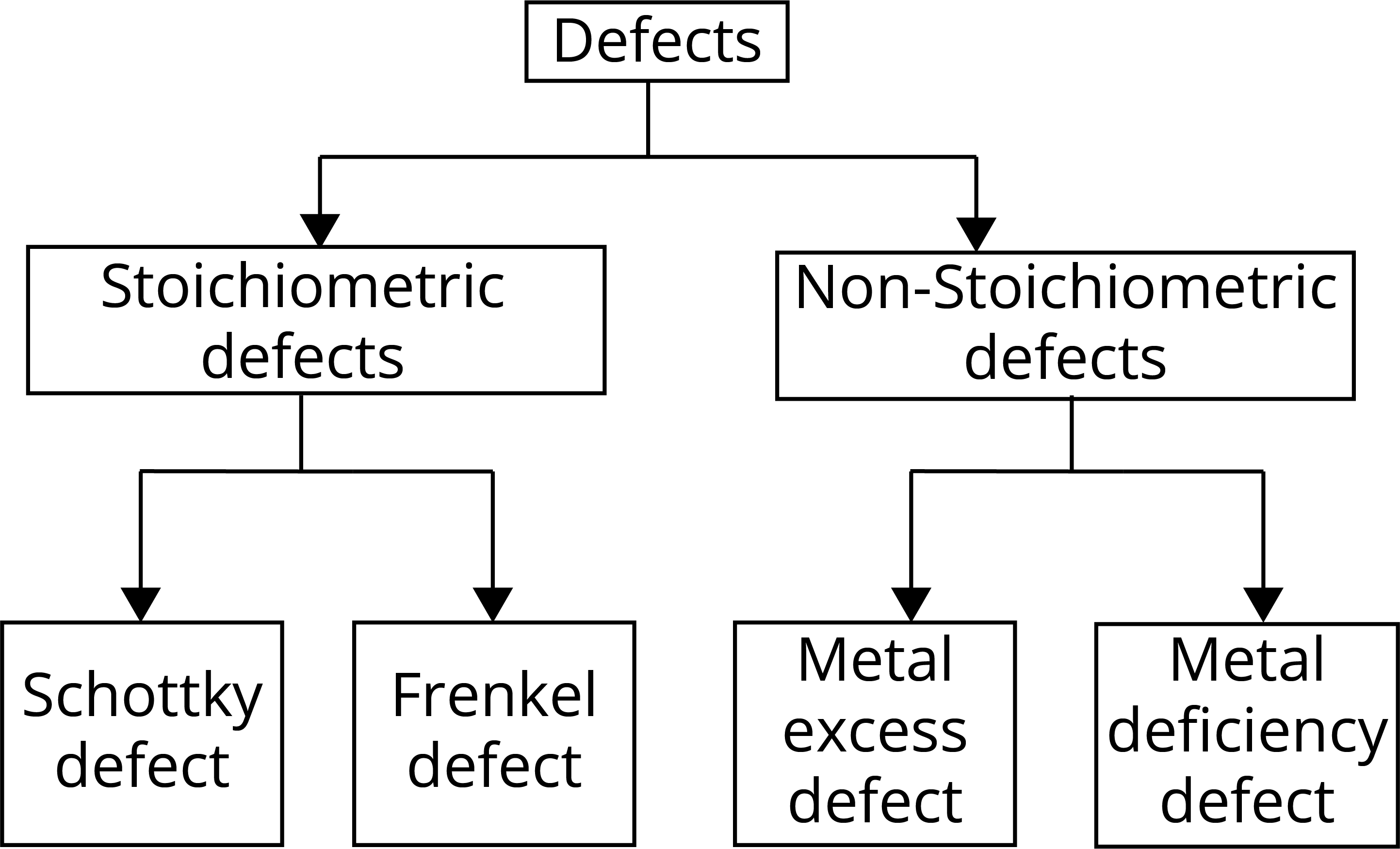
1. Stoichiometric Defects: These defects do not change the stoichiometry of the solid. There are two types of stoichiometric defects:

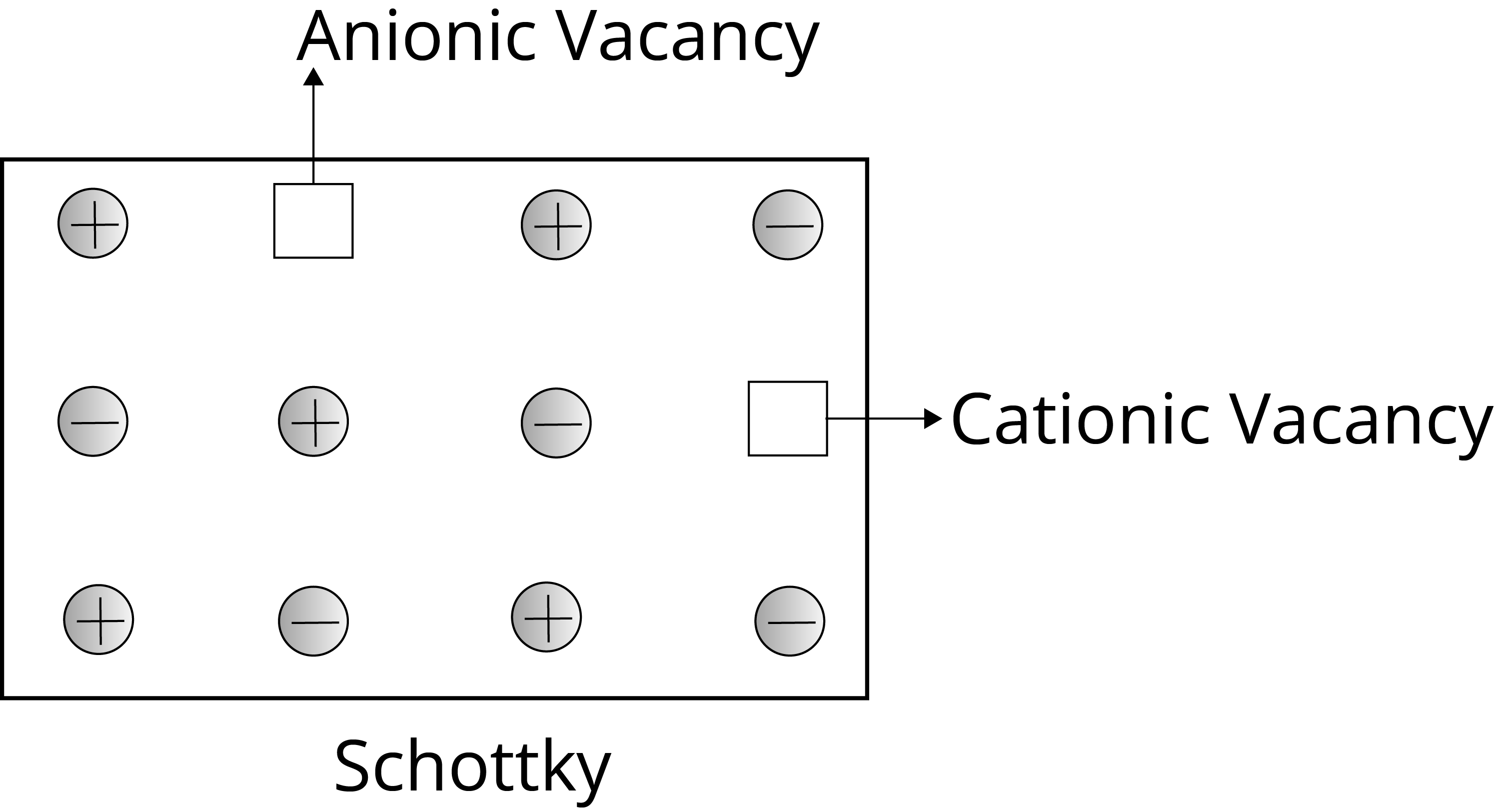
• The Schottky Defect: It is a vacancy defect in which the number of missing cations and anions in the crystal are equal. In this defect, electrical neutrality is maintained but the density of the crystal is decreased. The cations and anions of similar size show this type of defect, for example- KCl, NaCl, AgBr etc.
  
  

• Frenkel Defects: It is the dislocation defect in which the smaller ion is dislocated from its normal position to an interstitial site. The density of the crystal does not change. This type of defect is shown by the ionic solids in which the ions have large differences in size, for example- ZnS, AgCl, AgBr, and AgI.
  
  

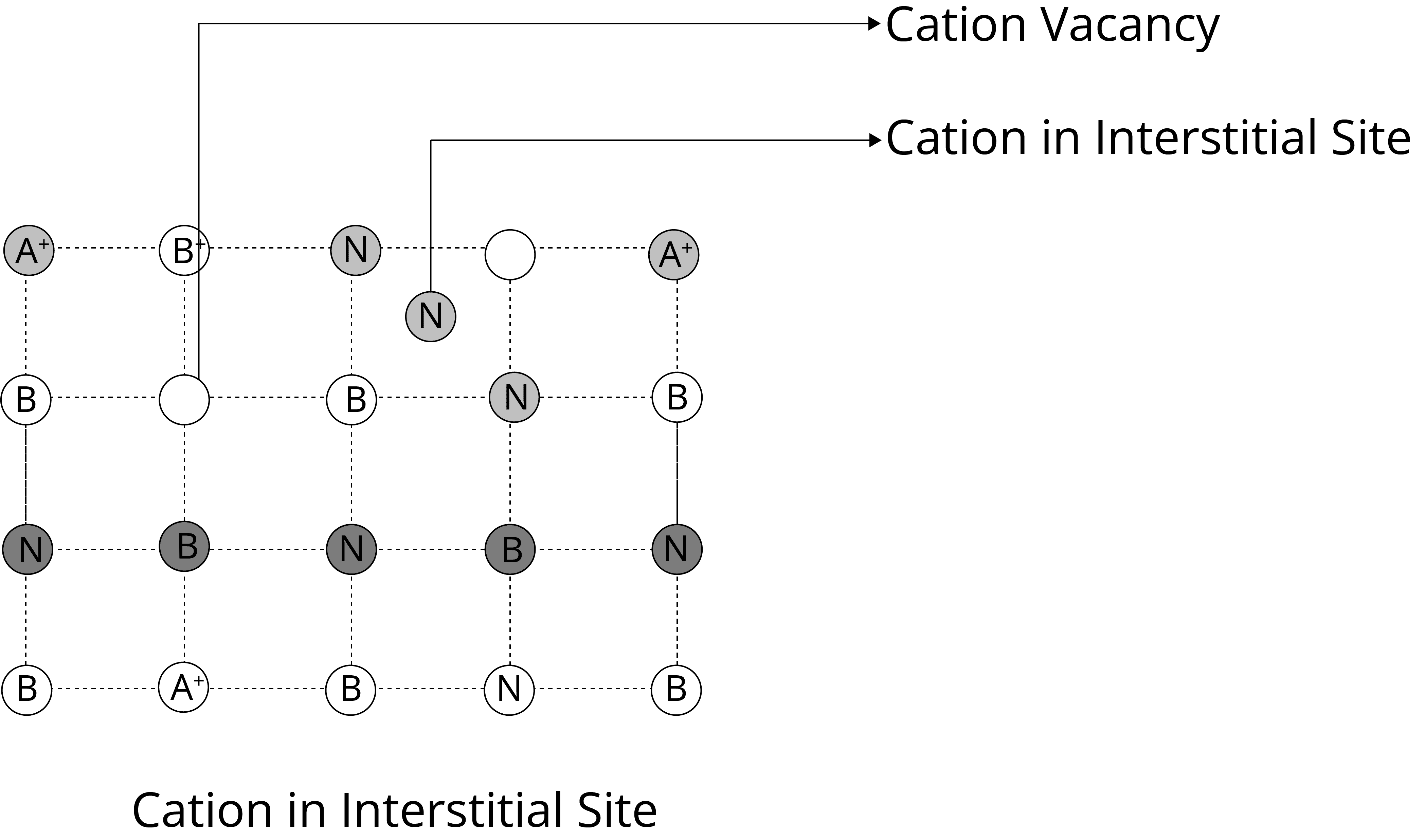
2. Non-Stoichiometric Defects: These defects do not change the stoichiometry of the solid. There are two types of non-stoichiometric defects:

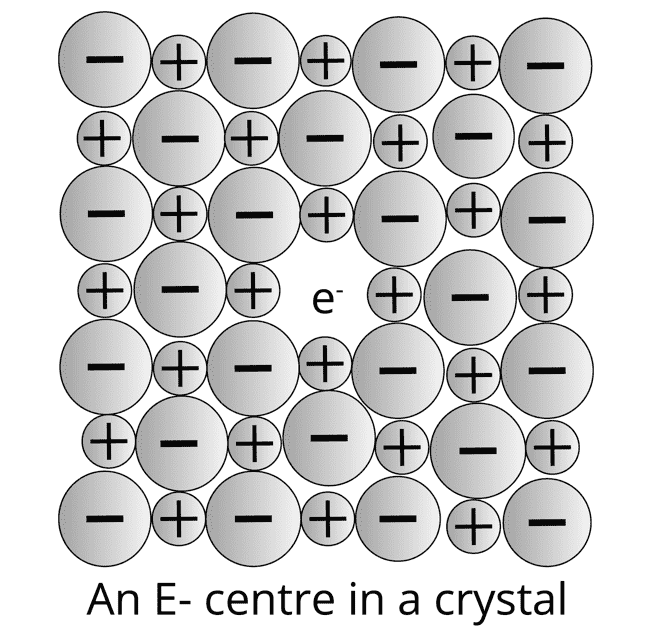
• Metal Excess Defect: In this defect, an anion is absent from its lattice position, leaving an electron behind to keep the charge balanced. The site that contains electrons is known as the F centre. They impart colour to the crystal example: NaCl appears yellow, LiCl appears pink and KCl appears lilac (or violet) in excess of their corresponding cationic metal due to metal excess defect.
  
  

• Metal Deficiency Defect: This defect occurs due to variable valency is shown by some metals for example FeO which occur in varying composition Fe0.93O to Fe0.96O. In FeO crystals some of the Fe2+ ion is missing from the crystal and the charge is balanced by Fe3+ ion.
  
  

Solved Examples From the Chapter

Example 1: A metal (atomic mass = 50) has a body-centered cubic crystal structure. The density of the metal is 5.96 g cm-3. Find the volume of the unit cell (NA =  6.023 x 1023 atoms mol-1).  : 

1. 1.56  X 10 -20cm3

2. 2.24 X 10-22cm3

3. 2.78 X 10 -23 cm3

4. 5.45 X 10-25cm3

Solution: (c) Given,  M = 50
                  ρ = 5.96 g cm-
                  Z = 2 (for BCC)
                  NA = 6.023 x 1023
                  V = ?

We know, ρ = $\dfrac{M \times Z}{V \times N_A}$

                  V   = $\dfrac{M \times Z}{ρ \times N_A}$

                       = $\dfrac{50 \times 2}{5,96 \times 6.023 \times 10 ^{23}}$

                       = 2.78  X  10 -23

Key points: Density of cubic crystals is given by formula:

Density,  ρ = $\dfrac{M \times Z}{a^{3}N_A}$

                 V = a3

Example 2: The atomic radius of nickel is 124 pm. Nickel crystallizes in a face-centered cubic lattice. What is the length of the edge of the unit cell? 

1. 430.2 pm

2. 350.7 pm

3. 213.8 pm

4. 620.5 pm

Solution:  (b) Given, r = 124 pm

Edge length, a = ?

$\sqrt{2}$a = 4r

a = 2$\sqrt{2}$r

a  =  2$\sqrt{2}$ X  124 pm  =  350.7 pm

Key Points: 

r = $\dfrac{\sqrt{2}a}{4}$

Solved Questions from the Previous Year Question Papers

Question 1: The parameters of the unit cell of a substance are a = 2.5, b = 3.0, c = 4.0; 

α = 90°, β = 120°, γ = 90°. The crystal system of the substance is : 

1. Hexagonal 

2. Orthorhombic

3. Monoclinic

4. Triclinic 

Solution: (c)  According to the question, a ≠ b ≠ c and  α = γ = 90° and β = 120°. The crystal system is monoclinic.

Question 2: A hard substance melts at high temperature and is an insulator in both solid and in molten state. This solid is most likely to be a/an : 

1. Covalent solid 

2. Molecular solid 

3. Ionic solid 

4. Metallic solid 

Solution: (a) Covalent solids are generally hard substances and melt at very high temperatures. They are insulators in both solid and molten states (except graphite).

Question 3: A diatomic molecule X2 has a body-centred cubic (bcc) structure with a cell edge of 300 pm. The density of the molecule is 6.17 g cm-3. The number of molecules present in 200 g of X2 is 

(Avogadro constant (NA)= 6 x 1023 mo1-1 ) 

(a) 8 NA

(b) 40 NA

(c) 4 NA

(d) 2 NA

Solution:  (c) Given, a = 300 pm = 3 X 10-8

ρ = 6.17 g cm-3

m = 200 g

Z  =  2(for BCC)

ρ = $\dfrac{M \times Z}{a^{3}N_A}$

6.17  =   $\dfrac{M \times 2}{(3 \times 10^{-8})^{3}   \times 10^{23}}$

M  =     50 g / mol

Number of moles = m/M  =  200/50  = 4

Number of molecules = 4 NA

Practice Questions

Question 1: Which of the following compounds is likely to show both Frenkel and Schottky defects in its crystalline form?  

1. CsCl

2. AgBr

3. ZnS

4. KBr

Answer: (b) AgBr

Question 2: The ratio of the number of atoms present in a simple cubic, body-centred cubic and face centred cubic structure are, respectively : 

1. 8 : 1 : 6

2. 4 : 2 : 1

3. 1 : 2 : 4

4. 4 : 2 : 3

Answer: (c)  1 : 2 : 4

Conclusion

In this article, we get to know that solids are more common than liquids and gases in our environment, and we use them more frequently. Solids with a wide range of characteristics are required for various applications. These characteristics are determined by the composition of the constituent particles as well as the binding forces that exist between them. As a result, studying the structure of solids is crucial. The structure and qualities of solids justify their uses for many purposes.