Mechanical Properties of Fluids an Important Concept for NEET
Mechanical Properties of Fluids is an important section as far as NEET is concerned. In this chapter we covered all mechanical properties and characteristics of fluid (liquid and gasses) and discussed how fluids are different from solids.
Fluid mechanics are considered as two types. First is fluid statics in which fluid or liquid is stationary (not moving). So in this part we have studied pressure, variation of pressure with depth or height and buoyancy force.
Another part is fluid dynamics in which we have studied about the dynamic nature of fluid and in this section is covered continuity equation, bernoulli equation etc.
The problems with continuity equations, Bernoulli equations are of frequently asked for the NEET exam.
In the later we also discussed the real fluid and their characteristics like viscosity, surface tension and excess pressure and also understand the important concept of surface energy. Let us see what topic and concept of mechanical properties of fluids are important for the NEET Exam with solved examples.
Mechanical Properties of Fluids - Important Topics
Mechanical properties of fluids notes
Pascal’s Law
mechanical properties of fluids formulas
Continuity Equation
Bernoulli’s Principle
mechanical properties of fluids solutions
properties of fluid - Viscosity
Stokes Law
Surface Energy
Important Concepts of Mechanical Properties of Fluids
Name of the Concept | Key Points of the Concept |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
List of Important Formulae
Sl. No | Name of the Concept | Formula |
1. | Pressure at h depth | |
2. | Buoyancy force | Here ρ is density of liquid g is acceleration due to gravity V is Volume of unmerged body or volume of displaced water |
3. | Equation of continuity | Here A is the area and v is the velocity |
4. | Bernoulli Equation | Here ρ is density of liquid g is acceleration due to gravity h is height and v is the velocity |
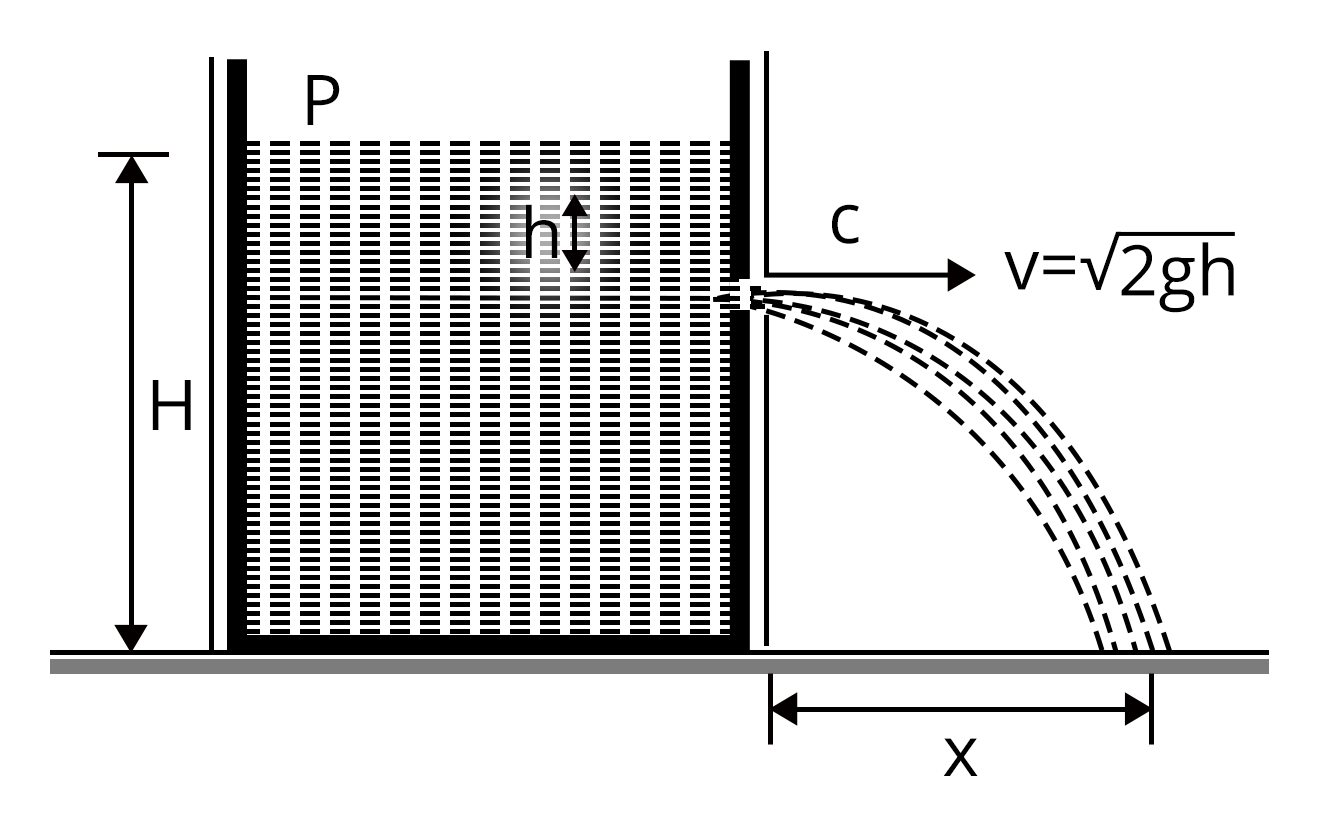
5. | Velocity of efflux | It is the velocity of liquid that will come out of a hole at h height from the bottom of the container filled with liquid
Here h is the height of hole from top. |
6. | Newton' law of viscosity (viscous force ) | Here η i viscosity |
7. | Drag force or viscous drag force | Here η is viscosity , v is velocity of object (spherical ) in the liquid and r is radius of spherical object |
8. | Terminal velocity | Here is density of object and is density of liquid |
9. | Surface energy | Surface energy = surface tension ✕ Area |
10. | Excess pressure inside a liquid drop | Here S is surface tension and r is radius |
11. | Excess pressure inside a soup bubble | Here S is surface tension and r is radius |
12. | Renold number | Here D is diameter of pipe and v is velocity |
13. | Capillary rise (height rise and height fall ) | Here Here ρ is density of liquid Θ is contact angle S is surface tension r is radius of capillary tube |
Solved Examples
1. A 100 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter of 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Ans:
Given mass of the girl = 100 kg
The diameter of the heel is d = 1 cm
The radius of the heel is = d/2 = 0.005 m
Now find area of the heel = A =
A = =
Due to heel the force on the floor would be F = mg = = 980 N
Pressure exerted by the heel on the floor by formula -
Trick - For determining pressure find the normal force acting on the surface then divide it by area of surface.
2. Torricelli's barometer used mercury. Pascal duplicated it using French wine of density 984 kg . Determine the height of the wine column for normal atmospheric pressure?
Ans:
We know that the density of mercury,
Density of French wine
We know that height of the mercury column, = 76 mm = 0.76 m
Let consider the height of the wine column =
We know that Acceleration due to gravity, g = 9.8
Pressure in both column mercury and wine is equal so
Key Point: Since both the liquid are at same atmospheric pressure therefore pressure remains the same for both the liquid.
Previous Year Questions from NEET Paper
1. A capillary tube of radius r is immersed in water and water rises in it to a height at the mass of the water in the capillary is 5 gram another capillary tube of radius 2r is immersed in water. The mass of water that will rise in this cube is (NEET 2020)
Ans:
Given - radius of capillary tube is - r
Mass of the water in the capillary is - 5 gm
New radius of capillary tube is - 2r
Change in pressure -
Multiply the whole equation by
Here ρ is density of liquid (water), g is acceleration due to gravity, r is radius of tube and V is the volume.
By the formula of density
M = ρV
Therefore M is proportional to the radius of the tube.
The mass of water that will rise in this cube is two times of 5 = 10 gm
Trick - In this type of question try to make the relation between given and required physical quantity.
2. A small hole of an area of cross-section is present near the bottom of a fully filled open tank of height 2 m. Taking g=10 , the rate of flow of water through the open hole would be nearly:
Ans:
Given - Area of cross section = A =
The rate of flow = Q = Av
Velocity = v =
=Q =
=
=
=
Trick - remember all the important formulas and see what is given and what we have to find then apply the relevant formula. In this question, think about the continuity equation and formula of rate of flow of fluid.
Practice Questions
Water falls down from a water tap with speed 3 m/s from 2 area then find area of streamline line when water goes down 80 cm (Ans: 1.2 )
Pressure of water in a pipe when tap is open is and it become when it is closed then what is velocity of flow when tap was open? (Ans: 10 m/s)
Conclusion
In this article, we discussed important topics , important Mechanical Properties of Fluid formulas from the NEET point of view. Students must make sure that they do not miss any of the above important topics to obtain a good score in the NEET exam.
NEET Important Chapter - Mechanical Properties of Fluids

 Share
ShareFAQs on NEET Important Chapter - Mechanical Properties of Fluids
1. How many questions are asked from Mechanical Properties of Fluid in NEET?
About 1-2 questions from this chapter are asked for NEET. It corresponds to around 8 marks in the NEET Exam.
2. How to get a good score in the NEET Exam ?
NEET Exam is not a very tough exam to crack. All you have to do is learn the concepts and solve all the questions in NCERT, CBSE class 11 and class 12 along with solving last 20 years previous year NEET question papers.
3. Are previous year questions enough for NEET Exam?
Students must prepare for this chapter by solving previous year questions and with help of NCERT books. Appear for NEET mock examination for preparation for any exam. And try to give sufficient time to revision.




















 Watch Video
Watch Video