NCERT Solutions for Class 11 Maths Chapter 3 - In Hindi

Exercise 3.1

1. निम्नलिखित डिग्री माप के संगत रेडियन माप ज्ञात कीजिए।

(i) $25^{\circ}$

(ii) $-47^{\circ} 30^{\prime}$

(iii) $240^{\circ}$

(iv) $520^{\circ}$

उत्तर: 

(i) $180^{\circ}=\pi$ रेडियन

$25^{\circ}=\frac{\pi}{180} \times 25=\frac{5\pi}{36}$ रेडियन।

(ii)$60^{\prime}=1^{\circ}$तब $30^{\prime}=\left(\frac{30}{60}\right)^{\circ}=\left(\frac{1}{2}\right)^{0}$

$\therefore \quad-47^{\circ} 30^{\prime}=\left(-47 \frac{1}{2}\right)^{\circ}=\left(-\frac{95}{2}\right)^{\circ}$

अब

$180^{\circ}=\pi$ रेडियन

$\therefore \quad\left(-\frac{95}{2}\right)^{\circ}-=\frac{-\pi}{180} \times \frac{95}{2}$ रेडियन

$=-\frac{19 \pi}{72}$ रेडियन।

$\therefore \quad-47^{\circ} 30^{\prime}=-\frac{19 \pi}{72}$ रेडियन

(iii) $\because$ $180^{\circ}=\pi$ रेडियन $240^{\circ}=\frac{\pi}{180} \times 240$ रेडियन $=\frac{4 \pi}{3}$ रेडियन।

(iv) $\because$ $180^{\circ}=\pi$ रेडियन $520^{\circ}=\frac{\pi}{180} \times 520$ रेडियन $=\frac{26 \pi}{9}$ रेडियन।

2. निम्नलिखित रेडियन माप के संगत डिग्री माप ज्ञात कीजिए $\left(\pi=\frac{22}{7}\right.$) का प्रयोग करें:

(i) $\frac{11}{16}$

(ii) $-4$

(iii) $\frac{5 \pi}{3}$

(iv) $\frac{7 \pi}{6}$

उत्तर: 

(i) $\pi$ रेडियन $=\frac{22}{7}$ रेडियन $=180^{\circ}$

$\frac{11}{16}$ रेडियन $=\frac{180}{22} \times 7 \times \frac{11}{16}$ िग्री

$=\frac{315}{8} \text { डिग्री }=39 \frac{3}{8} \text { डिग्री }$

$=39^{\circ}\left(\frac{3}{8} \times 60\right)^{\prime}$

$=39^{\circ} 22^{\prime}\left(\frac{1}{2} \times 60\right)^{n}$

$=39^{\circ} 22^{\prime} 30^{\prime \prime}$

(ii) $\frac{22}{77} \text { रेडिगन }=180^{\circ}$

$-4 \text { रेडियन }=\frac{180}{22} \times 7 \times(-4) \text { डिग्री }$

$=-\frac{2620}{11} \text { डिगी }$

$=-229^{\circ}\left(\frac{1}{11} \times 60\right)^{\prime}$

$=-229^{\circ} 5^{\prime}\left(\frac{5}{11} \times 60\right)^{\prime \prime}$

$=-229^{\circ} 5^{\prime} 27^{\prime \prime}($ निकटतम)|

(iii) $\pi$ रेडियन $=180^{\circ}$

$\therefore \quad \frac{5 \pi}{3}$ रेडियन $=\frac{180}{\pi} \times \frac{5 \pi}{3}=300^{\circ}$.

(iv) $\quad \pi$ रेडियन $=180^{\circ}$

$\therefore \quad \frac{7 \pi}{6}$ रेडियन $=\frac{180}{\pi} \times \frac{7 \pi}{6}=210^{\circ}$.

3. एक-पहिया एक मिनट में 360 परिक्रमण करता है तो एक सेकंड में कितने रेडियन माप का कोण बनाएगा?

उत्तर:

एक परिक्रमण में पहिया द्वारा बना कोण $=2\pi $ रेडियन

360 परिक्रमण में पहिया द्वारा बना कोण $=360 \times 2 \pi$ रेडियन

1 मिनट अर्थात् 60 सेकण्ड में $360 \times 2 \pi$ रेडियन का कोण बनता है।

1 सेकण्ट में चहिया द्वारा बना कोण $=\frac{360 \times 2 \pi}{60}$

$=12 \pi$ रेडियन।

4. एक वृत्त जिसकी त्रिज्या 100 सेमी है, 22 सेमी लंबाई की चाप वृत्त के केन्द्र पर कितने डिग्री माप का कोण बनाएगी ? $\left(\pi=\frac{22}{7}\right.$ का प्रयोग कीजिए)

उत्तर: 

$\because$ चाप = त्रिज्या $\times$ कोण

जहाँ चाप, 22 सेमी 

त्रिज्या, $r=100 सेमी $

$22=100 \times \theta$

$\theta=\frac{22}{100} रेडियन $

$=\frac{22}{100} \times \frac{180}{\pi} डिग्री $

$=\frac{22}{100} \times \frac{180}{22} \times 7 डिग्री $

$=\frac{63}{5} डिग्री $

$=12.6 डिग्री $

$=12^{\circ} 36^{\prime}$

5. एक वृत्त जिसका व्यास 40 सेमी. है, की एक जीवा 20 सेमी. लंबाई की है तो इसके संगत छोटे चाप की लंबाई ज्ञात कीजिए। 

उत्तर:

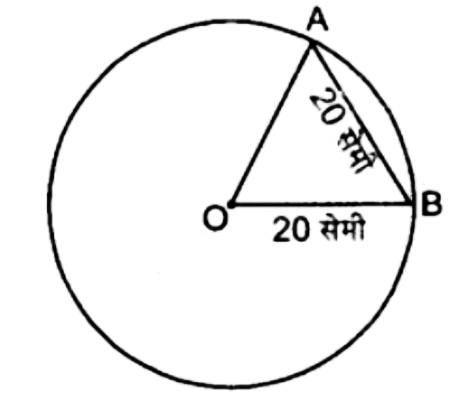
व्यास $=40$ सेमी 

त्रिज्या $=20$ सेमी

त्रिभुज $O A B$ एक समबाहु त्रिभुज है

$\angle A O B=60^{\circ}$

$=\frac{60 \times \pi}{180}$रेडियन

$=\frac{\pi}{3}$ रेडियन

मान लीजिए चाप $A B=l$.

केन्द्र $O$ पर चाप द्वारा बना कोण, $\theta=\frac{\pi}{3}$ रेडियन 

चाप AB की लम्बाई,

$=r \theta=20 \times \frac{\pi}{3}$रेडियन

$=\frac{20 \pi}{3}$ रेडियन।

6. यदि दो वृत्तों के समान लंबाई वाले चाप अपने केन्द्रों पर क्रमशः $60^{\circ}$ तथा $75^{\circ}$ के कोण बनाते हों, तो उन्क त्रिज्याओं को अनुपात ज्ञात कीजिए।

उत्तर:

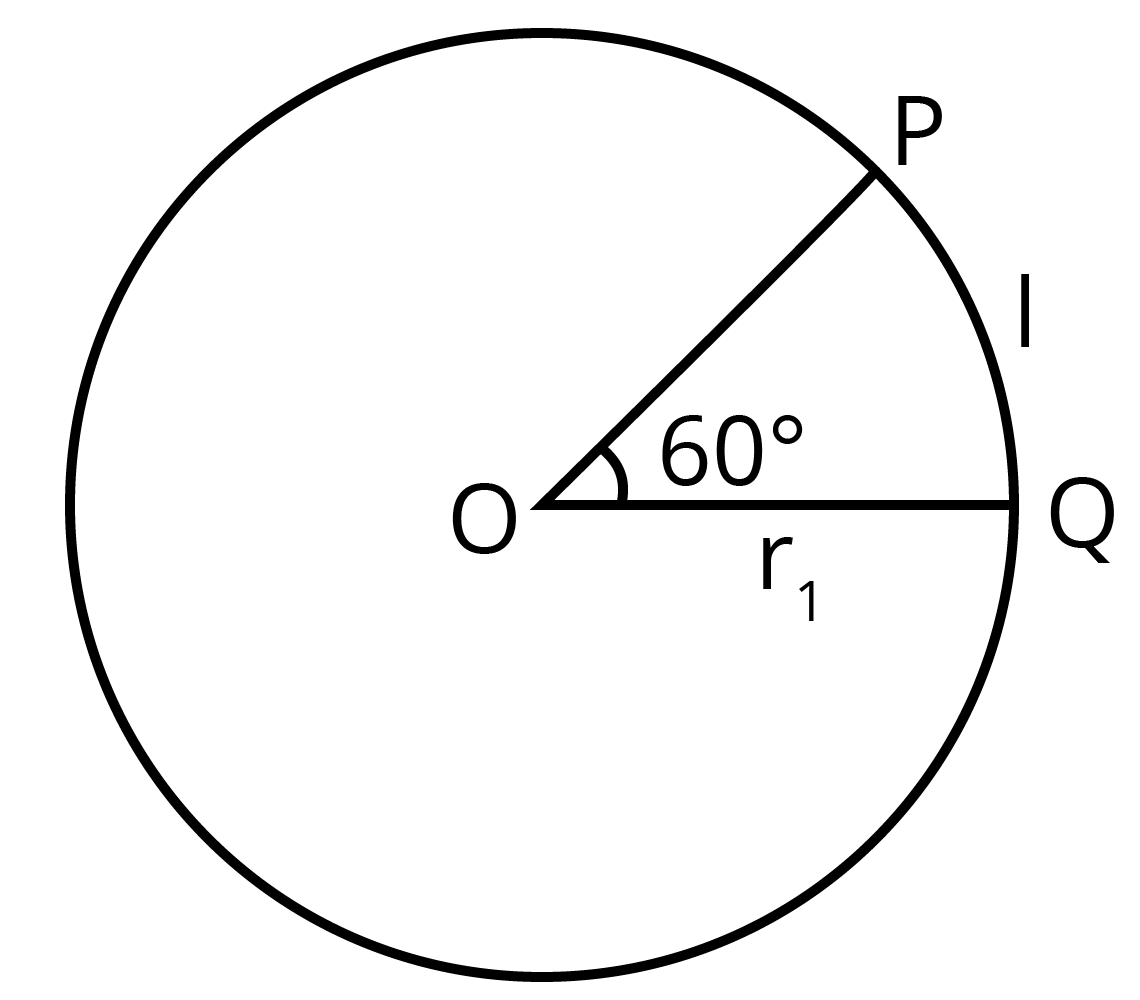
माना चाप की लंबाई $=l$

चाप द्वारा केन्द्र पर बना कोण $\theta_{1}=60^{\circ}$

$=\frac{\pi}{3}$ रेडियन

मान लीजिए इसकी त्रिज्या $=r_{1}$

$I =r_{1} \theta_{1}$

$=: r_{1} \frac{\pi}{3}$

$r_{1}=\frac{3 l}{\pi}$

दूसरे वृत्त के लिए,

माना त्रिज्या $=r_{2}$

चाप की लंबाई =।

चाप द्वारा केन्द्र पर बना कोण, $\theta_{2}=75^{\circ}$

$=75 \times \frac{\pi}{180}$ रेडियन

$=\frac{5 \pi}{12}$ रेडियन

$r_{2}=\frac{12 l}{5 \pi}$

समीकरण (i) को समीकरण (ii) से विभाजित करने पर

$\frac{r_{1}}{r_{2}}=\frac{3 l}{\pi} \div \frac{12 l}{5 \pi}$

$=\frac{3 l}{\pi} \times \frac{5 \pi}{12 l}=\frac{5}{4}=5: 4$

7. 75 सेमी लम्बाई वाले एक दोलायमान दोलक का एक सिरे से दूसरे सिरे तक दोलन करने से जो कोण बनता है, उसका माप रेडियन में ज्ञात कीजिए, जबकि उसके नोक द्वारा बनाए गए चाप की लम्बाई निम्नलिखित हैं:

(i) 10 सेमी

(ii) 15 सेमी

(iii) 21 सेमी

उत्तर:त्रिज्या $=75$ सेमी

(i) चाप की लम्बाई $l_{1}=10$ सेमी

यदि चाप द्वारा केन्द्र पर बना कोण $\theta$ रेडियन हो, तो

$l_{1}=r \theta_{1}$

$10=75 \theta_{2}$

$\theta_{1}=\frac{10}{75}=\frac{2}{15}$ रेडियन।

(ii)$r=75$ सेमी तथा $l_{2}=15$ सेमी

$l_{2}=r \theta_{2}$

$\theta_{2}=\frac{l_{2}}{r}=\frac{15}{75}=\frac{1}{5}$ रेडियन।

(iii)$\therefore$

$l_{3}=21$ सेमी, $r=75$ सेमी

$\theta_{3}=\frac{l_{3}}{r}=\frac{21}{75}$ रेडियन

$=\frac{7}{25}$ रेडियन ।

प्रश्नावली 3.2

निम्नलिखित प्रश्नों में पाँच अन्य त्रिकोणमतीय फलनों का मान ज्ञात कीजिए

1. $\mathbf{\cos x=-\frac{1}{2}, x}$ तीसरे चतुर्थांश में स्थित है।

उत्तर: $\cos \mathrm{x}=-\frac{1}{2}$

$\sin ^{2} x=1-\cos ^{2} x=1-\left(-\frac{1}{2}\right)^{2}=\frac{3}{4} \Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$

$\mathrm{x}$ तीसरे चतुथाश में स्थित है

$\Rightarrow \sin x=-\frac{\sqrt{3}}{2}$

$\operatorname{cosec} x=\frac{1}{\sin x}=-\frac{2}{\sqrt{3}}$

$\sec x=\frac{1}{\cos x}=-2$

$\tan x=\frac{-\frac{\sqrt{3}}{2}}{-\frac{1}{2}}=\sqrt{3}$

$\cot x=\frac{1}{\tan x}=\frac{1}{\sqrt{3}}$

2. $\mathbf{\sin \mathrm{x}=\frac{3}{5}, \mathrm{x}}$ दूसरे चतुर्थाश में स्थित है।

उत्तर: $\sin \mathrm{x}=\frac{3}{5}$

$\cos ^{2} x=1-\sin ^{2} x=1-\left(\frac{3}{5}\right)^{2}=\frac{16}{25} \Rightarrow \cos x=\pm \frac{4}{5}$

$\mathrm{x}$ दूसरे चतुथाश में स्थित है

$\Rightarrow \cos x=-\frac{4}{5}$

$\operatorname{cosec} x=\frac{1}{\sin x}=\frac{5}{3}$

$\sec x=\frac{1}{\cos x}=-\frac{5}{4}$

$\tan x=\frac{\frac{3}{5}}{-\frac{4}{5}}=-\frac{3}{4}$

$\cot x=\frac{1}{\tan x}=-\frac{4}{3}$

3. $\mathbf{\cot x=\frac{3}{4}, x}$ तीसरे चतुर्थांश में स्थित है।

उत्तर: $\cot \mathrm{x}=\frac{3}{4}$

$\operatorname{cosec}^{2} x=1+\cot ^{2} x=1+\left(\frac{3}{4}\right)^{2}=\frac{25}{16} \Rightarrow \operatorname{cosec} x=\pm \frac{5}{4}$

$\mathrm{x}$ तीसरे चतुथाश में स्थित है

$\Rightarrow \operatorname{cosec} x=-\frac{5}{4}$

$\sin x=\frac{1}{\operatorname{cosec} x}=-\frac{4}{5}$

$\cos ^{2} x=1-\sin ^{2} x=1-\left(-\frac{4}{5}\right)^{2}=\frac{9}{25} \Rightarrow \cos x=-\frac{3}{5}$

$\sec x=\frac{1}{\cos x}=-\frac{5}{3}$

$\tan x=\frac{1}{\tan x}=\frac{4}{3}$

4. $\mathbf{\sec \mathrm{x}=\frac{13}{5}, \mathrm{x}}$ चतुर्थ चतुथाश में स्थित है।

उत्तर:$\sec\mathrm{x}=\frac{13}{5}\Rightarrow \cos \mathrm{x}=\frac{5}{13}$

$\sin ^{2} x=1-\cos ^{2} x=1-\left(\frac{5}{13}\right)^{2}=\frac{144}{169}$

$\Rightarrow \sin x=\pm \frac{12}{13}$

$\mathrm{x}$ चतुर्थ चतुथंश में स्थित है

$\Rightarrow \sin x=-\frac{12}{13}$

$\operatorname{cosec} x=\frac{1}{\sin x}=-\frac{13}{12}$

$\tan x=\frac{\frac{5}{13}}{-\frac{12}{13}}=-\frac{5}{12}$

$\cot x=\frac{1}{\tan x}=-\frac{12}{5}$

5. $\mathbf{\tan \mathrm{x}=-\frac{5}{12}, \mathrm{x}}$ दूसरे चतुर्थांश में स्थित है।

उत्तर: $\tan \mathrm{x}=-\frac{5}{12}$

$\sec ^{2} x=1+\tan ^{2} x=1+\frac{25}{144}=\frac{169}{144} \Rightarrow \sec x=\pm \frac{13}{12}$

$\mathrm{x}$ दूसरे चतुर्थंश में स्थित है

$\sec x=-\frac{13}{12}$

$\Rightarrow \cos x=-\frac{12}{13}$

$\sin ^{2} x=1-\cos ^{2} x=1-\left(-\frac{12}{13}\right)^{2}=\frac{25}{169}$

$\Rightarrow \sin x=\pm \frac{5}{13}$

$\Rightarrow \sin x=\frac{5}{13}$

$\operatorname{cosec} x=\frac{1}{\sin x}=\frac{13}{5}$

$\cot x=\frac{1}{\tan x}=-\frac{12}{5}$

प्रश्र संख्या 6 से 10 का मान ज्ञात कीजिए।

6. $\mathbf{\sin 765^{\circ}}$

उत्तर:$\sin 765^{\circ}=\sin \left(2 \times 360^{\circ}+45\right)$

$=\sin 45^{\circ}$ [पहले चतुथंश मे $\sin$ धनात्मक होता है $]$

$=\frac{1}{\sqrt{2}}$

7. $\mathbf{\operatorname{cosec}\left(-1410^{\circ}\right)}$

उत्तर:$\operatorname{cosec}\left(-1410^{\circ}\right)=-\operatorname{cosec}\left(1410^{\circ}\right)$

$=-\operatorname{cosec}\left(4\times360^{\circ}-30^{\circ}\right)=-\left(-\operatorname{cosec}\left(30^{\circ}\right)\right)$

[चतुर्थ चतुर्थाश मे cosec ऋणात्मक होता है] $=2$

8. $\mathbf{\tan \frac{19 \pi}{3}}$

उत्तर:$\tan \frac{19 \pi}{3}=\tan \left(6 \pi+\frac{\pi}{3}\right)=\tan \frac{\pi}{3}$ [पहले चतुर्थांश मे tan धनात्मक होता है ] $=\sqrt{3}$

9. $\mathbf{\sin \left(\frac{-11 \pi}{3}\right)}$

उत्तर: $\sin \left(\frac{-11 \pi}{3}\right)=-\sin \left(\frac{11 \pi}{3}\right)$ $=-\sin\left(4 \pi-\frac{\pi}{3}\right)=-\left(-\sin \left(\frac{\pi}{3}\right)\right)$

[चतुर्थचतुर्थांशमे$\sin$ ऋणात्मक होता है।]$=\sin \left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}$

10. $\mathbf{\cot \left(\frac{-15 \pi}{4}\right)}$

उत्तर: $\cot \left(-\frac{15 \pi}{4}\right)=-\cot \left(\frac{15 \pi}{4}\right)$

$=-\cot \left(4 \pi-\frac{\pi}{4}\right)=-\left(-\cot \left(\frac{\pi}{4}\right)\right)$ [चतुर्थ चतुर्थांश मे cot ऋणात्मक होता है]

$=1$

प्रश्रावली 3.3

सिद्ध कीजिए :

1. $\mathbf{\sin ^{2} \frac{\pi}{6}+\cos ^{2} \frac{\pi}{3}-\tan ^{2} \frac{\pi}{4}=-\frac{1}{2}}$

उत्तर: $\sin ^{2} \frac{\pi}{6}+\cos ^{2} \frac{\pi}{3}-\tan ^{2} \frac{\pi}{4}=\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}-1$

$=\frac{1}{4}+\frac{1}{4}-1$

$=\frac{1}{2}-1=-\frac{1}{2}$

2. $\mathbf{2 \sin ^{2} \frac{\pi}{6}+\operatorname{cosec} \frac{7 \pi}{6} \cos ^{2} \frac{\pi}{3}=\frac{3}{2}}$

उत्तर: $2 \sin ^{2} \frac{\pi}{6}+\operatorname{cosec}^{2} \frac{7 \pi}{6} \cos ^{2}\frac{\pi}{3}=2\left(\frac{1}{2}\right)^{2}+\operatorname{cosec}^{2}\left(\pi+\frac{\pi}{6}\right) \times\left(\frac{1}{2}\right)^{2}$ $=\frac{1}{2}+2^{2} \times \frac{1}{4}=\frac{1}{2}+1=\frac{3}{2}$

3. $\mathbf{\cot ^{2} \frac{\pi}{6}+\operatorname{cosec}^{2} \frac{5 \pi}{6}+3 \tan ^{2} \frac{\pi}{6}=6}$

उत्तर: $\cot ^{2} \frac{\pi}{6}+\operatorname{cosec} \frac{5 \pi}{6}+3 \tan ^{2} \frac{\pi}{6}=(\sqrt{3})^{2}+\operatorname{cosec}\left(\pi-\frac{\pi}{6}\right)+3 \times\left(\frac{1}{\sqrt{3}}\right)^{2}$ $=3+\operatorname{cosec} \frac{\pi}{6}+1=4+2=6$

4. $\mathbf{2 \sin ^{2} \frac{3 \pi}{4}+2 \cos ^{2} \frac{\pi}{4}+2 \sec ^{2} \frac{\pi}{3}=10}$

उत्तर: $2 \sin ^{2} \frac{3 \pi}{4}+2 \cos ^{2} \frac{\pi}{4}+2 \sec ^{2} \frac{\pi}{3}=2 \sin ^{2}\left(\pi-\frac{\pi}{4}\right)+2\left(\frac{1}{\sqrt{2}}\right)^{2}+2(2)^{2}$ $=2 \sin ^{2} \frac{\pi}{4}+1+8=1+9=10$

5. मान ज्ञात कीजिए

(i) $\mathbf{\sin 75^{\circ}}$

उत्तर: $\sin 75^{\circ}=\sin \left(30^{\circ}+45^{\circ}\right)=\sin 45^{\circ} \cos 30^{\circ}+\cos 45^{\circ} \sin 30^{\circ}$

$[\sin (x+y)=\sin x \cos y+\cos x \sin y]$

$=\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}} \times \frac{1}{2}=\frac{1+\sqrt{3}}{2 \sqrt{2}}$

(ii) $\mathbf{\tan 15^{\circ}}$

उत्तर:$\tan 15^{\circ}=\tan \left(45^{\circ}-30^{\circ}\right)=\frac{\tan 45^{\circ}-\tan 30^{\circ}}{1+\tan 45^{\circ} \tan 30^{\circ}} \quad\left[\tan (\mathrm{x}-\mathrm{y})=\frac{\tan \mathrm{x}-\tan \mathrm{y}}{1+\tan \mathrm{x} \tan \mathrm{y}}\right]$

$=\frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}=\frac{\sqrt{3}-1}{\sqrt{3}+1}$

$=\frac{(\sqrt{3}-1)^{2}}{2}=\frac{2(2-\sqrt{3})}{2}=2-\sqrt{3}$

निम्रलिखित को सिद्ध कीजिए :

6.$\mathbf{\cos\left(\frac{\pi}{4}-x\right)\cos\left(\frac{\pi}{4}-y\right)-\sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right)=\sin (x+y)}$

उत्तर: $\cos \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-y\right)-\sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right)$ 

$=\cos \left(\frac{\pi}{4}-x+\frac{\pi}{4}-y\right) \quad(\cos A \times \cos B-\sin A \times \sin B=\cos (A+B))$ 

$=\cos \left(\frac{\pi}{2}-(x+y)\right)=\sin (x+y)$

7.$\mathbf{\frac{\tan\left(\frac{\pi}{4}+x\right)}{\tan\left(\frac{\pi}{4}-x\right)}=\left(\frac{1+\tan x}{1-\tan x}\right)^{2}}$

उत्तर:$\frac{\tan\left(\frac{\pi}{4}+\mathrm{x}\right)}{\tan\left(\frac{\pi}{4}-\mathrm{x}\right)}$

$=\frac{\frac{1+\tan x}{1-1 \times \tan x}}{\frac{1-\tan x}{1+1 \times \tan x}}$

$={\left[\frac{1+\tan x}{1-\tan x}\right)^{2}}$

8. $\mathbf{\frac{\cos (\pi-x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\cot ^{2} x}$ 

उत्तर: $\frac{\cos (\pi-x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\frac{-\cos (x) \cos (x)}{\sin (x)(-\sin (x))}$ $=\frac{\cos ^{2} x}{\sin ^{2} x}=\cot ^{2} x$

9. $\mathbf{\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]=1}$ 

उत्तर: $\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]$

$=\sin x \cos x\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]$

$=\sin x \cos x[\tan x+\cot x]$

$=\sin x \cos x\left(\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right)$

$=\sin x \cos x\left(\frac{1}{\sin x \cos x}\right)=1$

10. $\mathbf{\sin (n+1) x \sin (n+2) x+\cos (n+1) x \cos (n+2) x=\cos x}$

उत्तर: $\sin (n+1) x \sin (n+2) x+\cos (n+1) x \cos (n+2) x$

$=\cos ((n+1) x-(n+2) x) \quad[\cos A \times \cos B+\sin A \times \sin B=\cos (A-B)]$

$=\cos (-x)=\cos x$

11.$\mathbf{\cos\left(\frac{3\pi}{4}+x\right)-\cos\left(\frac{3\pi}{4}-x\right)=-\sqrt{2} \sin x}$

उत्तर: $\operatorname{Cos}\left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi}{4}-x\right)$

$=-2 \sin \left(\frac{\left(\frac{3 \pi}{4}+x\right)+\left(\frac{3 \pi}{4}-x\right)}{2}\right) \sin \left(\frac{\left(\frac{3 \pi}{4}+x\right)-\left(\frac{3 \pi}{4}-x\right)}{2}\right)$

${\left[\cos (a+b)-\cos (a-b)=-2 \sin \left(\frac{a+b}{2}\right) \sin \left(\frac{a-b}{2}\right)\right]}$

$=-2 \sin \left(\frac{3 \pi}{4}\right) \sin x=-2 \sin \left(\pi-\frac{\pi}{4}\right) \sin x$

$=-2 \times \frac{1}{\sqrt{2}} \sin x=-\sqrt{2} \sin x$

12. $\mathbf{\sin ^{2} 6 x-\sin ^{2} 4 x=\sin 2 x \sin 10 x}$

उत्तर:  $\sin ^{2} 6 \mathrm{x}-\sin ^{2} 4 \mathrm{x}=(\sin 6 \mathrm{x}+\sin 4 \mathrm{x})(\sin 6 \mathrm{x}-\sin 4 \mathrm{x}$ )

$=2 sin (\frac{6 x+4 x}{2}) cos (\frac{6 x-4 x}{2}) 2 sin (\frac{6 x -4 x}{2}) cos (\frac{6 x+4 x}{2})$

$=(2 \sin 5 \mathrm{x} \cos \mathrm{x})(2 \cos 5 \mathrm{x} \sin \mathrm{x})$

$=(2 \sin x \cos \mathrm{x})(2 \sin 5 \mathrm{x} \cos 5 \mathrm{x})$

$=\sin 2 \mathrm{x} \sin 10 \mathrm{x}$

13. $\boldsymbol{\mathbf{}\cos ^{2} 2 x-\cos ^{2} 6 x=\sin 4 x \sin 8 x}$

उत्तर: $\cos ^{2} 2 \mathrm{x}-\cos ^{2} 6 \mathrm{x}=(\cos 2 \mathrm{x}+\cos 6 \mathrm{x})(\cos 2 \mathrm{x}-\cos 6 \mathrm{x})$

$=2 cos (\frac{2 x+6 x}{2}) cos (\frac{2x-6 x}{2}) -2 sin (\frac{2 x -6 x}{2}) sin (\frac{2 x+6 x}{2})$

$=(2 \cos 4 \mathrm{x} \cos 2 \mathrm{x})(2 \sin 4 \mathrm{x} \sin 2 \mathrm{x})$

$=(2 \sin 2 \mathrm{x} \cos 2 \mathrm{x})(2 \sin 4 \mathrm{x} \cos 4 \mathrm{x})=\sin 4 \mathrm{x} \sin 8 \mathrm{x}$

14. $\mathbf{\sin 2 x+2 \sin 4 x+\sin 6 x=4 \cos ^{2} x \sin 4 x}$

उत्तर: $\sin 2 \mathrm{x}+2 \sin 4 \mathrm{x}+\sin 6 \mathrm{x}$

$=2 \sin \left(\frac{6 x+2 x}{2}\right) \cos \left(\frac{6 x-2 x}{2}\right)+2 \sin 4 x$

$=2 \sin 4 x(1+\cos 2 x)=2 \sin 4 x\left(1+2 \cos ^{2} x-1\right)$

$=4 \cos ^{2} x \sin 4 x$

15. $\mathbf{\cot 4 x(\sin 5 x+\sin 3 x)=\cot x(\sin 5 x-\sin 3 x)}$

उत्तर: $\cot 4 \mathrm{x}(\sin 5 \mathrm{x}+\sin 3 \mathrm{x})=\cot \mathrm{x}(\sin 5 \mathrm{x}-\sin 3 \mathrm{x})$

दायाँ पक्ष $=\cot 4 \mathrm{x}(\sin 5 \mathrm{x}+\sin 3 \mathrm{x})$

$=\frac{\cos 4 x}{\sin 4 x}\left(2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)\right)$ $=\frac{\cos 4 x}{\sin 4 x}(2 \sin 4 x \cos x)=2 \cos 4 x \cos x$ बायाँ पक्ष $=\cot x(\sin 5 x-\sin 3 x)$

$=\frac{ cos x}{ sin x} 2 sin (\frac{5 x-3 x}{2}) cos (\frac{5 x+3 x}{2})$

$=\frac{\cos \mathrm{x}}{\sin \mathrm{x}}(2 \sin \mathrm{x} \cos 4 \mathrm{x})=2 \cos 4 \mathrm{x} \cos \mathrm{x}=$दायाँ पक्ष

दायाँ पक्ष = बायाँ पक्ष

16. $\mathbf{\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}}$

उत्तर: $\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=\frac{-2 \sin \left(\frac{9 x+5 x}{2}\right) \sin \left(\frac{9 x-5 x}{2}\right)}{2 \cos \left(\frac{17 x+3 x}{2}\right) \sin \left(\frac{17 x-3 x}{2}\right)}$ $=-\frac{2 \sin 7 x \sin 2 x}{2 \cos 10 x \sin 7 x}=-\frac{\sin 2 x}{\cos 10 x}$

17. $\mathbf{\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}=\tan 4 x}$

उत्तर: $\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}=\frac{2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)}{2 \cos \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)}$

$=\frac{2 \sin 4 x \cos x}{2 \cos 4 x \cos x}$

$=\frac{\sin 4 x}{\cos 4 x}=\tan 4 x$

18. $\mathbf{\frac{\sin x-\sin y}{\cos x+\cos y}=\tan \left(\frac{x-y}{2}\right)}$

उत्तर: $\frac{\sin x-\sin y}{\cos x+\cos y}=\frac{2 \sin \left(\frac{x-y}{2}\right) \cos \left(\frac{x+y}{2}\right)}{2 \cos \left(\frac{x-y}{2}\right) \cos \left(\frac{x+y}{2}\right)}$

$=\frac{\sin \left(\frac{x-y}{2}\right)}{\cos \left(\frac{x-y}{2}\right)}$

$=\tan \left(\frac{x-y}{2}\right)$

19. $\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}=\tan 2 x$

उत्तर: $\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}=\frac{2 \sin \left(\frac{x+3 x}{2}\right) \cos \left(\frac{x-3 x}{2}\right)}{2 \cos \left(\frac{x+3 x}{2}\right) \cos \left(\frac{x-3 x}{2}\right)}$

$=\frac{2 \sin 2 x \cos (-x)}{2 \cos 2 x \cos (-x)}$

$=\frac{\sin 2 x}{\cos 2 x}=\tan 2 x$

20. $\mathbf{\frac{\sin x-\sin 3 x}{\sin ^{2} x-\cos ^{2} x}=2 \sin x}$

उत्तर: $\frac{\sin x-\sin 3 x}{\sin ^{2} x-\cos ^{2} x}=\frac{2 \sin \left(\frac{x-3 x}{2}\right) \cos \left(\frac{x+3 x}{2}\right)}{-\left(\cos ^{2} x-\sin ^{2} x\right)}$

$=\frac{2 \sin (-x) \cos (2 x)}{-\cos 2 x}$

$=\frac{-2 \sin x \cos (2 x)}{-\cos 2 x}=2 \sin x$

21. $\mathbf{\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}=\cot 3 x}$

उत्तर: $\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}=\frac{2 \cos \left(\frac{4 x+2 x}{2}\right) \cos \left(\frac{4 x-2 x}{2}\right)+\cos 3 x}{2 \sin \left(\frac{4 x+2 x}{2}\right) \cos \left(\frac{4 x-2 x}{2}\right)+\sin 3 x}$

$=\frac{2 \cos 3 x \cos x+\cos 3 x}{2 \sin 3 x \cos x+\sin 3 x}$

$=\frac{\cos 3 x(2 \cos x+1)}{\sin 3 x(2 \cos x+1)}=\frac{\cos 3 x}{\sin 3 x}$

$=\cot 3 x$

22. $\mathbf{\cot x \cot 2 x-\cot 2 x \cot 3 x-\cot 3 x \cot x=1}$

उत्तर: $\cot 3 \mathrm{x}=\cot (2 \mathrm{x}+\mathrm{x})=\frac{\cot 2 \mathrm{x} \cot \mathrm{x}-1}{\cot \mathrm{x}+\cot 2 \mathrm{x}}$ $\Rightarrow \cot 3 x(\cot x+\cot 2 x)=\cot 2 x \cot x-1$

$\Rightarrow \cot 3 x \cot x+\cot 3 x \cot 2 x=\cot 2 x \cot x-1$

$\Rightarrow \cot x \cot 2 x-\cot 2 x \cot 3 x-\cot 3 x \cot x=1$

23. $\mathbf{\tan 4 x=\frac{4 \tan x\left(1-\tan ^{2} x\right)}{1-6 \tan ^{2} x+\tan ^{4} x}}$

उत्तर: $\tan 4 x=\tan 2(2 x)=\frac{2 \tan 2 x}{1-\tan ^{2} 2 x}=\frac{\frac{4 \tan x}{1-\tan ^{2} x}}{1-\left(\frac{2 \tan x}{1-\tan ^{2} x}\right)^{2}}$

$=\frac{4 \tan x\left(1-\tan ^{2} x\right)}{\left(1-\tan ^{2} x\right)^{2}-4 \tan ^{2} x}$

$=\frac{4 \tan x\left(1-\tan ^{2} x\right)}{1-2 \tan ^{2} x+\tan ^{4} x-4 \tan ^{2} x}=\frac{4 \tan x\left(1-\tan ^{2} x\right)}{1+\tan ^{4} x-6 \tan ^{2} x}$

24. $\mathbf{\cos 4 x=1-8 \sin ^{2} x \cos ^{2} x}$

उत्तर: $\cos 4 \mathrm{x}=\cos 2(2 \mathrm{x})=1-2 \sin ^{2} 2 \mathrm{x}$

$=1-2(2 \sin x \cos x)^{2}$

$=1-2\left(4 \sin ^{2} x \cos ^{2} x\right)$

$=1-8 \sin ^{2} x \cos ^{2} x$

25. $\mathbf{\cos 6 \mathrm{x}=32 \cos ^{6} \mathrm{x}-48 \cos ^{4} \mathrm{x}+18 \cos ^{2} \mathrm{x}-1}$

उत्तर: $\cos 6 \mathrm{x}=\cos 2(3 \mathrm{x})=2 \cos ^{2} 3 \mathrm{x}-1$

$=2\left(4 \cos ^{3} x-3 \cos x\right)^{2}-1$

$=2\left(16 \cos ^{6} x+9 \cos ^{2} x-24 \cos ^{4} x\right)-1$

$=32 \cos ^{6} x-48 \cos ^{4} x+18 \cos ^{2} x-1$

प्रश्रावली 3.4

निम्नलिखित समीकरणों का मुख्य तथा व्यापक हल ज्ञात कीजिए

1. $\mathbf{\tan x=\sqrt{3}}$

उत्तर: यह जाना जाता है कि $\tan \frac{\pi}{3}=\sqrt{3}$ और

$\tan \left(\frac{4 \pi}{3}\right)=\tan \left(\pi+\frac{\pi}{3}\right)=\tan \frac{\pi}{3}=\sqrt{3}$

इसलिए, प्रमुख उत्तर हैं $\mathrm{x}=\frac{\pi}{3}$ और $\frac{5 \pi}{3}$

अभी, $\tan \mathrm{x}=\tan \frac{\pi}{3}$

$\Rightarrow \mathrm{x}=\mathrm{n} \pi+\frac{\pi}{3}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

2. $\mathbf{\sec x=2}$

उत्तर: यह जाना जाता है कि $\sec \frac{\pi}{3}=2$ और

$\sec \frac{5 \pi}{3}=\sec \left(2 \pi-\frac{\pi}{3}\right)=\sec \frac{\pi}{3}=2$

इसलिए, प्रमुख उत्तर हैं $\mathrm{x}=\frac{\pi}{3}$ और $\frac{5 \pi}{3}$

अभी, $\sec x=\sec \frac{\pi}{3}$

$\Rightarrow \cos x=\cos \frac{\pi}{3} \Rightarrow 2 \mathrm{n} \pi \pm \frac{\pi}{3}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

इसलिए, सामान्य उत्तर है $\mathrm{x}=2 \mathrm{n} \pi \pm \frac{\pi}{3}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

3. $\mathbf{\cot x=-\sqrt{3}}$

उत्तर: यह जाना जाता है कि $\cot \frac{\pi}{6}=\sqrt{3}$

$\therefore \cot \left(\pi-\frac{\pi}{6}\right)=-\cot \frac{\pi}{6}=-\sqrt{3} \text { और } \cot \left(2 \pi-\frac{\pi}{6}\right)$

$=-\cot \frac{\pi}{6}=-\sqrt{3}$

i.e. $\cot \frac{5 \pi}{6}=-\sqrt{3}$ और $\cot \frac{11 \pi}{6}=-\sqrt{3}$

इसलिए, प्रमुख उत्तर हैं $\mathrm{x}=\frac{5 \pi}{6}$ और $\frac{11 \pi}{6}$

अभी, $\cot \mathrm{x}=\cot \frac{5 \pi}{6}$

$\Rightarrow \tan \mathrm{x}=\tan \frac{5 \pi}{6} \text { जहॉँ } \mathrm{n} \in \mathrm{Z}$

$\Rightarrow \mathrm{n} \pi+\frac{5 \pi}{6}$

इसलिए, सामान्य उत्तर है $\mathrm{x}=\mathrm{n} \pi+\frac{5 \pi}{6}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

4. $\boldsymbol{\mathbf{}\operatorname{cosec} x=-2}$

उत्तर: यह जाना जाता है कि $\operatorname{cosec} \frac{\pi}{6}=-2$

$\operatorname{cosec}\left(\pi+\frac{\pi}{6}\right)=-\operatorname{cosec} \frac{\pi}{6}=-2 \text { और } \operatorname{cosec}\left(2 \pi-\frac{\pi}{6}\right)$

$=-\operatorname{cosec} \frac{\pi}{6}=-2$

i.e. $\operatorname{cosec} \frac{7 \pi}{6}=-2$ और $\operatorname{cosec} \frac{11 \pi}{6}=-2$

इसलिए, प्रमुख उत्तर हैं $\mathrm{x}=\frac{7 \pi}{6}$ और $\frac{11 \pi}{6}$

अभी, $\operatorname{cosec} \mathrm{x}=\operatorname{cosec} \frac{7 \pi}{6}$

$\Rightarrow \sin \mathrm{x}=\sin \frac{7 \pi}{6} \Rightarrow \mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{7 \pi}{6}$, जहाँ $\mathrm{n} \in \mathrm{Z}$

इसलिए, सामान्य उत्तर है $\Rightarrow \mathrm{x}=\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{7 \pi}{6}$, जहाँ $\mathrm{n} \in \mathrm{Z}$

निम्नलिखित प्रत्येक समीकरणों का व्यापक हल ज्ञात कीजिए:

5. $\mathbf{\cos 4 x=\cos 2 x}$

उत्तर: $\cos 4 \mathrm{x}=\cos 2 \mathrm{x}$

$\Rightarrow \cos 4 x-\cos 2 x=0$

$\Rightarrow-2 \sin \left(\frac{4 x+2 x}{2}\right) \sin \left(\frac{4 x-2 x}{2}\right)=0$

$\Rightarrow\left[\therefore \cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A+B}{2}\right)\right]$

$\Rightarrow \sin 3 x=0 \text { या } \sin x=0$

$\therefore 3 x=n \pi \text { या } \sin x=0$

$\therefore 3 \mathrm{x}=\mathrm{n} \pi$ या $\mathrm{x}=\mathrm{n} \pi$ जहाँ $\mathrm{n} \in \mathrm{Z}$

$\Rightarrow \mathrm{x}=\frac{\mathrm{n} \pi}{3}$ या $\mathrm{x}=\mathrm{n} \pi$ जहा $\mathrm{n} \in \mathrm{Z}$

6. $\mathbf{\cos 3 x+\cos x-\cos 2 x=0}$

उत्तर: $\cos 3 \mathrm{x}+\cos \mathrm{x}-\cos 2 \mathrm{x}=0$

$2 \cos \left(\frac{3 x+x}{2}\right) \cos \left(\frac{3 x-x}{2}\right)-\cos 2 x=0$

$2 \cos 2 x \cos x-\cos 2 x=0$

$\cos 2 x(2 \cos x-1)=0$

$\Rightarrow \cos 2 x=0 \text { या } 2 \cos x-1=0$

$\Rightarrow \cos 2 x=0 \text { या } \cos x=\frac{1}{2}$

$\therefore 2 \mathrm{x}=(2 \mathrm{n}+1) \frac{\pi}{2}$ या $\cos \mathrm{x}=\cos \frac{\pi}{3}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

$\Rightarrow \mathrm{x}=(2 \mathrm{n}+1) \frac{\pi}{2}$ या $\mathrm{x}=2 \mathrm{n} \pi \pm \frac{\pi}{3}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

7. $\mathbf{\sin 2 \mathrm{x}+\cos \mathrm{x}=0}$

उत्तर: $\sin 2 \mathrm{x}+\cos  \mathrm{x}=0$

$2 \sin x \cos x+\cos x=0$

$\cos x(2 \sin x+1)=0$

अभी, $\cos \mathrm{x}=0 \Rightarrow \cos \mathrm{x}=(2 \mathrm{n}+1) \frac{\pi}{2}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

$2 \sin x+1=0$

$\Rightarrow \sin x=-\frac{1}{2}=-\sin \frac{\pi}{6}=\sin \left(\pi+\frac{\pi}{6}\right)=\sin \frac{7 \pi}{6}$

$\Rightarrow x=n \pi+(-1)^{n} \frac{7 \pi}{6} \text { जहाँ } n \in Z$

इसलिए, सामान्य उत्तर है $(2 \mathrm{n}+1) \frac{\pi}{2}$ या $\mathrm{x}=\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{7 \pi}{6}$

8. $\mathbf{\sec ^{2} 2 x=1-\tan 2 x}$

उत्तर: $\sec ^{2} 2 \mathrm{x}=1-\tan 2 \mathrm{x}$

$\Rightarrow 1+\tan ^{2} 2 \mathrm{x}=1-\tan 2 \mathrm{x}$

$\Rightarrow \tan ^{2} 2 \mathrm{x}+\tan 2 \mathrm{x}=0$

$\Rightarrow \tan 2 \mathrm{x}(\tan 2 \mathrm{x}+1)=0$

$\Rightarrow \tan 2 \mathrm{x}=0 \text { या } \tan 2 \mathrm{x}+1=0$

$\Rightarrow \tan 2 \mathrm{x}=\tan 0$

$\Rightarrow 2 \mathrm{x}=\mathrm{n} \pi+0$ जहाँ $\quad \mathrm{n} \in \mathrm{Z}$

$\Rightarrow \mathrm{x}=\frac{\mathrm{n} \pi}{2}$, जहाँ $\mathrm{n} \in \mathrm{Z}$

$\tan 2 \mathrm{x}+1=0$

$\Rightarrow \tan 2 \mathrm{x}=-1=-\tan \frac{\pi}{4}=\tan \left(\pi-\frac{\pi}{4}\right)=\tan \frac{3 \pi}{4}$

$\Rightarrow 2 \mathrm{x}=\mathrm{n} \pi+\frac{3 \pi}{4}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

$\Rightarrow \mathrm{x}=\frac{\mathrm{n} \pi}{2}+\frac{3 \pi}{8}$, जहाँ $\mathrm{n} \in \mathrm{Z}$

इसलिए, सामान्य उत्तर है $\mathrm{x}=\frac{\mathrm{n} \pi}{2}$ या $\mathrm{x}=\frac{\mathrm{n} \pi}{2}+\frac{3 \pi}{8}$ जहाँ $\mathrm{n} \in \mathrm{Z}$

9. $\mathbf{\sin x+\sin 3 x+\sin 5 x=0}$

उत्तर: $\sin x+\sin 3 x+\sin 5 x=0$

$(\sin x+\sin 5 x)+\sin 3 x=0$

$\Rightarrow\left[2 \sin \left(\frac{x+5 x}{2}\right) \cos \left(\frac{x-5 x}{2}\right)\right]+\sin 3 x=0$

$\Rightarrow 2 \sin 3 \mathrm{x} \cos (-2 \mathrm{x})+\sin 3 \mathrm{x}=0$

$\Rightarrow2 \sin 3 \mathrm{x} \cos 2 \mathrm{x}+\sin 3 \mathrm{x}=0$

$\Rightarrow \sin 3 \mathrm{x}(2 \cos 2 \mathrm{x}+1)=0$

$\Rightarrow \sin 3 \mathrm{x}=0 \text { या } 2 \cos 2 \mathrm{x}+1=0$

$\sin 3 \mathrm{x}=0 \Rightarrow 3 \mathrm{x}=\mathrm{n} \pi$, जहाँ $\mathrm{n} \in \mathrm{Z}$

i.e. $\mathrm{x}=\frac{\mathrm{n} \pi}{3}$, जहाँ $\mathrm{n} \in \mathrm{Z}$

$2 \cos 2 x+1=0$

$\Rightarrow \cos 2 x=\frac{-1}{2}=-\cos \frac{\pi}{3}=\cos \left(\pi-\frac{\pi}{3}\right)$

$\Rightarrow \cos 2 x=\cos \frac{2 \pi}{3}$

$\Rightarrow 2 x=2 n \pi \pm \frac{2 \pi}{3} \text { जहाँ } n \in Z$

$\Rightarrow x=n \pi \pm \frac{\pi}{3}, \text { जहाँ } n \in Z$

इसलिए, सामान्य उत्तर है $\mathrm{x}=\frac{\mathrm{n} \pi}{3}$ या $\mathrm{x}=\mathrm{n} \pi \pm \frac{\pi}{3} \mathrm{n} \in \mathrm{Z}$

प्रश्रावली A 3

सिद्ध कीजिए :

1. $\mathbf{2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=0}$

उत्तर: $2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=\cos \left(\frac{\pi}{13}+\frac{9 \pi}{13}\right)+\cos \left(\frac{\pi}{13}-\frac{9 \pi}{13}\right)+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}$ $[2 \cos x \cos y=\cos (x+y)+\cos (x-y)]$

$=\cos \frac{10 \pi}{13}+\cos \frac{8 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}$

$=\cos \left(\pi-\frac{3 \pi}{13}\right)+\cos \left(\pi-\frac{8 \pi}{13}\right)+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}$

$=-\cos \frac{3 \pi}{13}-\cos \frac{5 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=0$

2. $\mathbf{(\sin 3 x+\sin x) \sin x+(\cos 3 x-\cos x) \cos x=0}$

उत्तर: $(\sin 3 x+\sin x) \sin x+(\cos 3 x-\cos x) \cos x$

$=2 \sin \frac{3 x+x}{2} \cos \frac{3 x-x}{2} \sin x-2 \sin \frac{3 x+x}{2} \sin \frac{3 x-x}{2} \cos x=0$

$\because\left[\sin x+\sin y=2 \sin \frac{x+y}{2} \cos \frac{x-y}{2}, \cos x-\cos y=-2 \sin \frac{x+y}{2} \sin \frac{x-y}{2}\right]$

$=2 \sin 2 x \sin x \cos x-2 \sin 2 x \sin x \cos x$

$\quad \because[\sin 2 x=2 \sin x \cos x]$

$=(\sin 2 x)^{2}-(\sin 2 x)^{2}=0$

3. $\mathbf{(\cos x+\cos y)^{2}+(\sin x-\sin y)^{2}=4 \cos ^{2} \frac{(x+y)}{2}}$

उत्तर: $(\cos x+\cos y)^{2}+(\sin x-\sin y)^{2}=\left(2 \cos \frac{x+y}{2} \cos \frac{x-y}{2}\right)^{2}+\left(2 \cos \frac{x+y}{2} \sin \frac{x-y}{2}\right)^{2}$

$\because\left[\cos A+\cos B=2 \cos \frac{A+B}{2} \cos \frac{A-B}{2}, \sin A-\sin B=2 \cos \frac{A+B}{2} \sin \frac{A-B}{2}\right]$

$=4\left(\cos \frac{x+y}{2}\right)^{2}\left[\left(\cos \frac{x+y}{2}\right)^{2}+\left(\sin \frac{x+y}{2}\right)^{2}\right]$

$=4\left(\cos \frac{x+y}{2}\right)^{2} \quad \because\left[\sin ^{2} x+\cos ^{2} x=1\right]$

4. $\mathbf{(\cos x-\cos y)^{2}+(\sin x-\sin y)^{2}=4 \sin ^{2} \frac{(x-y)}{2}}$

उत्तर: $(\cos x-\cos y)^{2}+(\sin x-\sin y)^{2}=\left(-2 \sin \frac{x+y}{2} \sin \frac{x-y}{2}\right)^{2}+\left(2 \cos \frac{x+y}{2} \sin \frac{x-y}{2}\right)^{2}$

$\because\left[\cos A-\cos B=-2 \sin \frac{A+B}{2} \sin \frac{A-B}{2}, \sin A-\sin B=2 \cos \frac{A+B}{2} \sin \frac{A-B}{2}\right]$

$=4\left(\sin\frac{x-y}{2}\right)^{2}\left[\left(\cos\frac{x+y}{2}\right)^{2}+\left(\sin \frac{x+y}{2}\right)^{2}\right]$

$=4\left(\sin \frac{x-y}{2}\right)^{2} \quad \because\left[\sin ^{2} x+\cos ^{2} x=1\right]$

5. $\mathbf{\sin x+\sin 3 x+\sin 5 x+\sin 7 x=4 \cos x \cos 2 x \sin 4 x}$

उत्तर: $\sin x+\sin 3 x+\sin 5 x+\sin 7 x=(\sin x+\sin 7 x)+(\sin 3 x+\sin 5 x)$

$=2 \sin \frac{7 x+x}{2} \cos \frac{7 x-x}{2}+2 \sin \frac{5 x+3 x}{2} \cos \frac{5 x-3 x}{2}$

$\because\left[\sin x+\sin y=2 \sin \frac{x+y}{2} \cos \frac{x-y}{2}\right]$

$=2 \sin 4 x \cos 3 x+2 \sin 4 x \cos x=2 \sin 4 x(\cos 3 x+\cos x)$

$\because\left[\cos x+\cos y=2 \cos \frac{x+y}{2} \cos \frac{x-y}{2}\right]$

$=2 \sin 4 x\left(2 \cos \frac{3 x+x}{2} \cos \frac{3 x-x}{2}\right)=4 \sin 4 x \cos 2 x \cos x$

6. $\mathbf{\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)}=\tan 6 x}$

उत्तर: $\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)}$

$=\frac{2 \sin \frac{7 x+5 x}{2} \cos \frac{7 x-5 x}{2}+2 \sin \frac{9 x+3 x}{2} \cos \frac{9 x-3 x}{2}}{2 \cos \frac{7 x+5 x}{2} \cos \frac{7 x-5 x}{2}+2 \cos \frac{9 x+3 x}{2} \cos \frac{9 x-3 x}{2}}$

$=\frac{2 \sin 6 x \cos x+2 \sin 6 x \cos 3 x}{2 \cos 6 x \cos x+2 \cos 6 x \cos 3 x}$

$=\frac{\sin 6 x(\cos x+\cos 3 x)}{\cos 6 x(\cos x+\cos 3 x)}$

$=\frac{\sin 6 x}{\cos 6 x}$

$=\tan 6 x$

7. $\mathbf{\sin 3 x+\sin 2 x-\sin x=4 \sin x \cos \frac{x}{2} \cos \frac{3 x}{2}}$

उत्तर: $\sin 3 x+\sin 2 x-\sin x=(\sin 3 x-\sin x)+\sin 2 x$

$=2 \cos \frac{3 x+x}{2} \sin \frac{3 x-x}{2}+\sin 2 x$

$\because\left[\sin x-\sin y=2 \cos \frac{x+y}{2} \sin \frac{x-y}{2}\right]$

$=2 \cos 2 x \sin x+\sin 2 x=2 \cos 2 x \sin x+2 \cos x \sin x$

$=2 \sin x(\cos 2 x+\cos x)$

$=\left(2 \cos \frac{2 x+x}{2} \cos \frac{2 x-x}{2}\right)(2 \sin x)$

$=4 \sin x \cos \frac{3 x}{2} \cos \frac{x}{2}$

निम्नलिखित प्रत्येक प्रश्न $ \mathbf{sin(\frac{x}{2}), cos (\frac{x}{2}, tan(\frac{x}{2})}$में तथा ज्ञात कीजिए:

8. $\mathbf{\tan \mathrm{x}=-\frac{4}{3}, \mathrm{x}}$ द्वितीय चतुर्थाश में है।

उत्तर: दिया गया है $\tan \mathrm{x}=-\frac{4}{3}$

$\sec^{2}x=1+\tan^{2}x=1+\left(\frac{-4}{3}\right)^{2}=1+\left(\frac{16}{9}\right)=\frac{25}{9}$

$\sec x=\pm \frac{5}{3}$

चूकि $\mathrm{x}$ द्वितीय चतुथांश में है

अतः $\sec x=-\frac{5}{3}$

$\cos x=-\frac{3}{5}$

$\mathrm{x}$ द्वितीय चतुर्थांश में है

$\Rightarrow \frac{\pi}{2} \leq x \leq \pi$

$\Rightarrow \frac{\pi}{4} \leq \frac{x}{2} \leq \frac{\pi}{2}$

$\sin x / 2=\sqrt{(1-\cos x) / 2}=\sqrt{4 / 5}=\frac{2}{\sqrt{5}}$

$\cos x / 2=\sqrt{(1+\cos x) / 2}=\frac{1}{\sqrt{5}}$

$\tan x / 2=\frac{\sin x / 2}{\cos x / 2}=2$

9. $\mathbf{\cos x=-\frac{1}{3}, x}$ तृतीय चतुर्थांश में है।

उत्तर: दिया गया है, $\cos \mathrm{x}=-\frac{1}{3}$

चूकि $\mathrm{x}$ द्वितीय चतुथंश में है

अतः $\pi \leq \mathrm{x} \leq \frac{3 \pi}{2}$

$\frac{\pi}{2} \leq \frac{x}{2} \leq \frac{3 \pi}{4}$

$\sin x / 2=\sqrt{(1-\cos x) / 2}=\sqrt{4 / 6}=\frac{2}{\sqrt{6}}$

$=\sqrt{\frac{2}{3}}$

$\cos x / 2=\sqrt{(1+\cos x) / 2}=\pm \sqrt{2 / 6}=\pm \frac{1}{\sqrt{3}}$

चूकि $\mathrm{x}$ तृतीय चतुथांश में है

अतः $\cos \mathrm{x} / 2=-\frac{1}{\sqrt{3}}$

$\tan x / 2=\frac{\sin x / 2}{\cos x / 2}=-\sqrt{2}$

10. $\mathbf{\sin x=\frac{1}{4}, x}$ द्वितीय चतुर्थाश में है।

उत्तर: दिया गया है $\sin x=\frac{1}{4}$,

$\cos \mathrm{x}=\pm \sqrt{1-\sin ^{2} \mathrm{x}}=\pm \sqrt{1-\left(\frac{1}{4}\right)^{2}}=\pm \frac{\sqrt{15}}{4}$

चूकि $\mathrm{x}$ द्वितीय चतुथांश में है

अतः $\cos x=-\frac{\sqrt{15}}{4}$

$\sin x / 2=\sqrt{(1-\cos x) / 2}=\sqrt{\frac{4+\sqrt{15}}{8}}$

$\cos x / 2=\sqrt{(1+\cos x) / 2}=\sqrt{\frac{4-\sqrt{15}}{8}}$

चूकि $\mathrm{x}$ तृतीय चतुथंश में है

$\tan \mathrm{x} / 2=\frac{\sin \mathrm{x} / 2}{\cos \mathrm{x} / 2}=\frac{\sqrt{\frac{4+\sqrt{15}}{8}}}{\sqrt{\frac{4-\sqrt{15}}{8}}}$

$=\sqrt{\frac{4+\sqrt{15}}{4-\sqrt{15}}}\times\sqrt{\frac{4+\sqrt{15}}{4+\sqrt{15}}}=\frac{4+\sqrt{15}}{16-15}$

$=4+\sqrt{15}$