Volume Definition for Kids
Have you ever wondered why a football looks bigger than a tennis ball, or why a lake looks bigger than a bucket of water? It is because of the difference in their volumes. Volume is defined as the amount of space occupied by an object that is bound by a boundary. It must be noted that the volume is a mathematical term that is only applicable to 3D (three-dimensional) objects or spaces. As such, the units commonly used for volume are cubic units, that is, m3, cm3, in3, etc.
How Can We Find the Volume of Different Shapes?
Different geometric shapes have different volumes. The common 3D shapes that we come across in our daily lives are cubes, cuboids, spheres, cylinders, cones, etc.
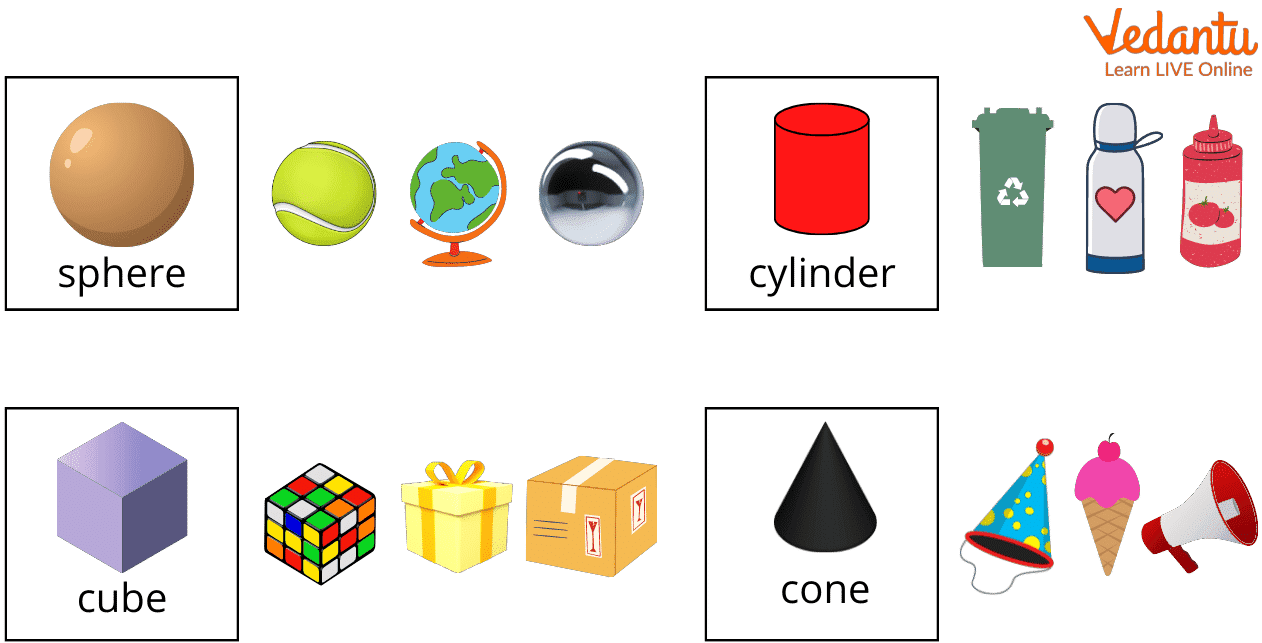
Real Life 3D Objects
In case of shapes having a flat surface, such as a cube or a cuboid, it is easy to find the volume. However, for curved shapes, like cones, cylinders, and spheres, it is required to consider the dimensions of their curved surfaces as well. For instance, their radii or diameters.
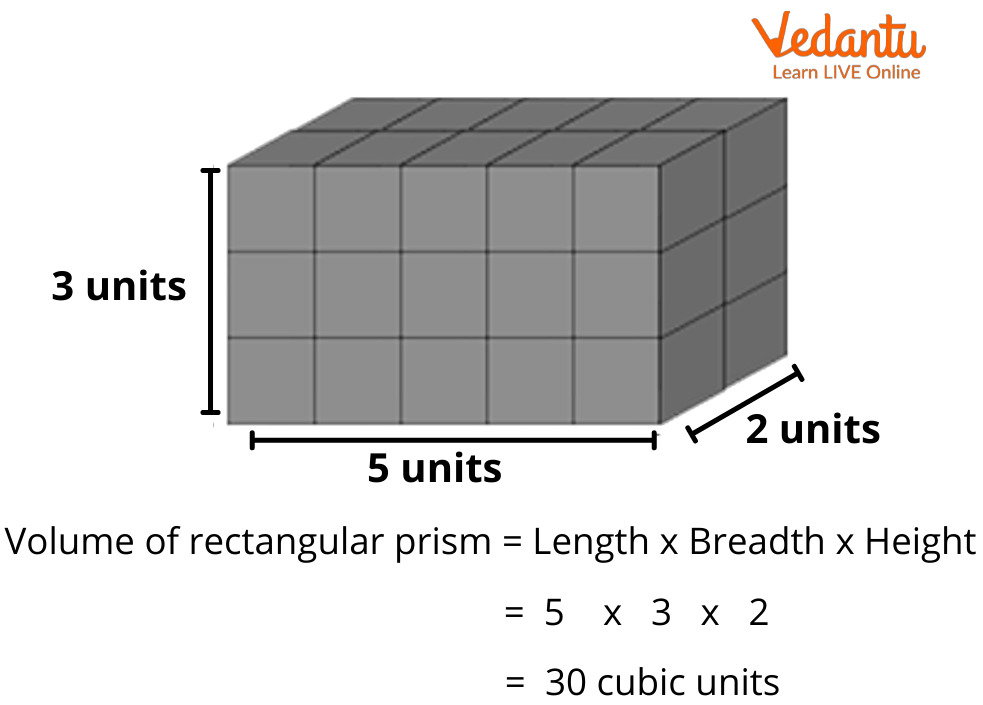
How to Calculate the Volume of a Prism?
The following is a table containing the formulas of volume for some commonly known regular shapes:
Sample Solutions for Finding Volume
Question 1: Determine the volume of a cube if its side length equals 3 cm.
Solution: It is given that the length of the cube = 3 cm.
As we know,
Volume of cube = Side3
Thus,
Volume of a cube with 3 cm length = 33 cm3
Volume = 27 cm3
Question 2: What is the volume of a cone if its radius is 2 cm and height is 5 cm?
Solution: It is given that the radius of the circular base of a cone = 2 cm
And the height of the cone = 5 cm
As we know,
Volume of cone = ⅓ πr2h
Volume = ⅓ π (2)2 (5)
Volume = ⅓ x 22/7 x 4 x 5
Volume = 20.95 cm3
Question 3: If the volume of a cube is 512 cm3, what will be its surface area?
Solution: Since a3 = 512
Therefore, a=∛(512)
a=8 cm
Surface area of Cube= 6a2
=(6 x 82 ) cm2
=384 cm2
Question 4: Calculate the volume of a hemisphere that has a radius of 3 cm.
Solution: Volume of the hemisphere = (2/3)πr3
= (2/3) x π x 33
= (2/3) x π x 27
= 18π cm3
Irregular Solids
Solids that do not have definite shapes or measurements are called irregular solids. Such solids do not usually have fixed formulas that can be used to determine their volumes. However, there are different ways to obtain such volumes, one of which is the liquid displacement method, which is based on the Archimedes Principle.
The method involves submerging an irregular solid in a container that is filled up to the brim with any liquid whose weight and volume are already known. The volume of liquid that is displaced will therefore be the required volume of the irregular solid. The said volume can be determined by pouring this displaced water into a container of regular shape, and it can be measured up.
Few Things to Note While Studying about Volume
Since all sides of a cube are equal, the volume will be equal to the cube of the length of its side.
In a case where the radius and height of a cone and a cylinder are the same, the volume of the cone will be equal to one-third of the volume of the cylinder.
The formulas of the volumes of a cuboid and a rectangular prism are the same.
The volume of a prism depends on the shape of its base. For instance, if the base is a square, the volume will be side2 x height.
Conclusion
To sum up, the capacity of an object to occupy three-dimensional space is known as its volume. The volume of certain regular objects is generally formulated as the product of the base and height of the objects. However, not all volumes of regular objects can be calculated in this manner. Also, finding the volume of irregular objects or masses that do not have a definite shape can be tricky, for which the liquid displacement method comes in handy.
FAQs on What is Volume?
1. What are irregular solids? Write some examples of irregular solids?
Solids without definite shapes or measurements are known as irregular solids. Examples of irregular solids can be stones, fruits, the human body, and other masses whose volume cannot be conventionally determined.
2. How can we calculate the volume of irregular objects?
There is an easy way to calculate the volume of irregular objects. The method includes submerging the irregular solid into a container filled to the brim with water or liquid of known weight, whose volume is previously known. The displaced volume of water will thus be the volume of the irregular solid. This volume can be easily obtained by pouring the displaced water into a regular shaped container and measuring it up. The principle used in this method is called the Archimedes Principle.