




How to Compare Numbers: Understanding “Larger” in Maths
It's vital to remember that every number on a number line is larger than the number to its left and less than the number to its right while learning greater than and less than symbols. In arithmetic, the terms larger or less than and equal are used to help children comprehend how one number differs from another. Whether one number is more than or less than the other, or whether both numbers are equal. Important symbols or signs are needed to identify numbers in order to comprehend the larger, smaller, and equal numbers.
What is Greater Than?
Inequality can be defined as a comparison between two or more numbers, quantities, or values. It's utilized when the first or second amount or number is more than the second or remainder quantity or number. When comparing numbers and values, the sign > is used. The sign's large open side always points to the larger number, while the little end always points to the smaller number.

Plane is Larger Than Bus and Cab
To compare integers and expressions, greater than and less than symbols can be employed. > is the greater than symbol. As a result, 9 >7 means '9 is greater than 7'. The sign for less than is. (greater than or equal to) and (less than or equal to) are two other comparison symbols (less than or equal to).
It appears to be a straightforward concept: larger than less than. We would discuss which number the "alligator" ate.
We use the greater than the symbol “>” when one integer is greater than the other.
We use the less-than sign “<” when one number is less than the other.
When one number equals another, we use the equal to symbol “=”.
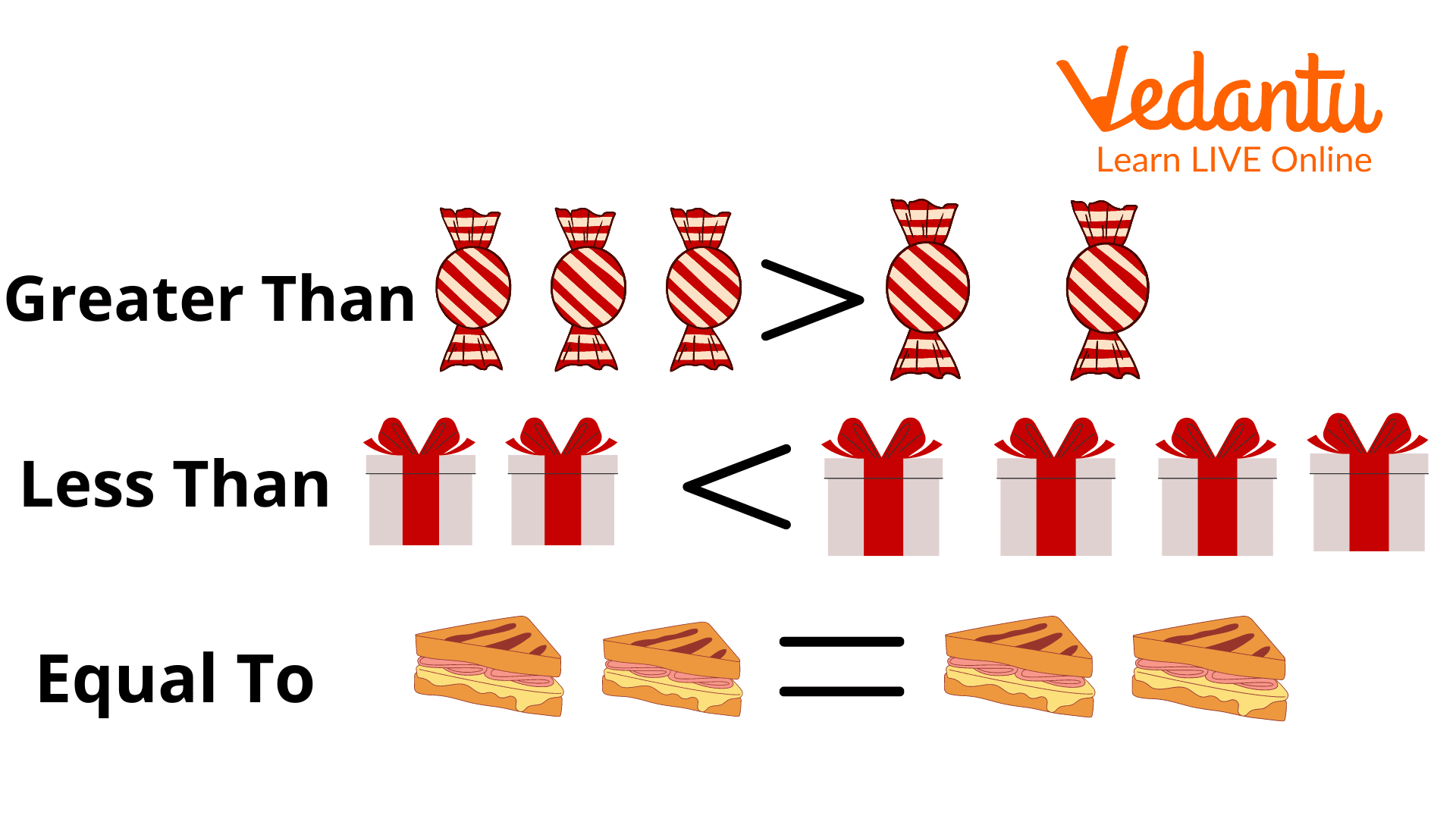
Greater Than, Less Than, and Equal to Signs.
> The open right hand is usually greater than the sign.
< The open left hand is usually greater than the sign.
Examples
8 is greater than 3
8 > 3
4 is less than 9
4 < 9
5 is equal to 5
5 = 5
Compare the numbers in each set and place a > sign between them.
45 > 39
89 > 12
27 > 23
100 > 95
50 > 30
Tips for Parents
Ask your child to compare the sizes of plates, glasses, and cups, describing the differences using words like "huge," "larger," and "largest."
Compare and contrast your child's hands and feet with your own. Ask who has the larger hand or foot by placing your hand or foot next to your child's. Inquire about the person with the smaller hand or foot.
Use your hands or feet to measure things around the house. "Could you tell me how many walls there are in the room?" Measure the height of the TV with your hands.
Conclusion
To represent the connection between two numbers, greater than and less than symbols are employed. It is vital to teach children the concepts of more and less so that they can compare the quantities of goods and determine which is more or less.
Toys, attractive objects, fruits, vegetables, and other stuff, rather than simply words, may be used to teach more and fewer ideas to children with autism. The wide-open side of the sign is always towards the higher-valued number. These symbols come in handy when there is no clear answer to an arithmetic issue.
FAQs on What Is Larger in Maths? Definition, Facts & Examples
1. How can I teach both large and small lessons to my child?
Toys that teach your child the distinction between big and little are wonderful for stacking and sorting. The distinction may be demonstrated with nested bowls or stacking rings. You can accomplish the same thing with everyday objects. Give your youngster a variety of plastic bowls, straws, and pencils in various sizes.
2. What is the significance of knowing more than or greater than?
To represent the connection between two numbers, greater than and less than symbols are employed. The sign's wide-open side is always towards the higher-valued number. These symbols are very useful in arithmetic problems with no obvious solution.

















