Unit Cubes Definition Formula and Volume Examples
Have you ever played the ludo? Yes! That is great. Then surely you have used dice. Isn't it? Can you tell the shape of a dice? Or, you might try to fix the Rubik’s Cube. What is the shape of a Rubik’s cube? The shape of both the objects is a ‘cube’. A cube is an object that has all edges equal in size. Can you count the number of edges a cube has? Yes, you are right, it is 12.
But the question is what is a unit cube? Let's read the complete article and get the answers to such questions.
What Is the Unit Cube?
Like any other cube, a unit cube is a three-dimensional object. It also has 12 edges. And, the major point to be focussed on is that the length of all edges is equal to 1 unit. A unit cube is also called a ‘Cube of Side 1’. It has six faces which are unit squares.
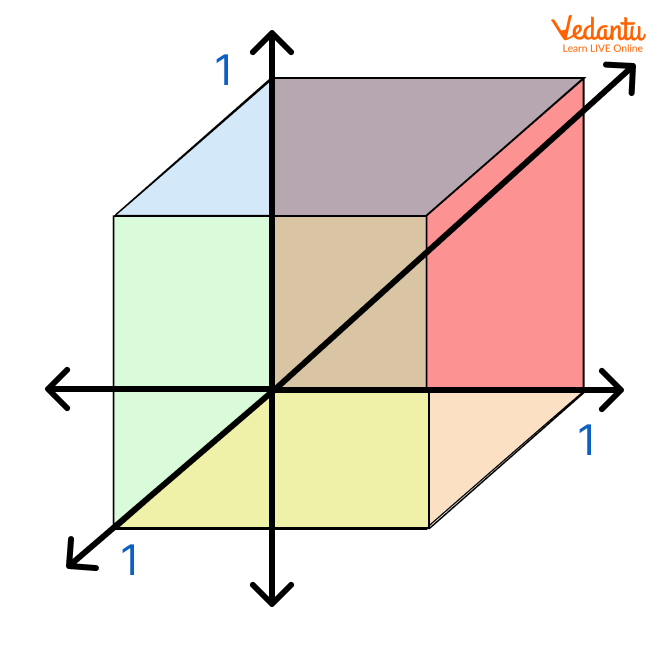
Unit Cube
The Volume of a Unit Cube
We know that the volume of a cube is calculated as:
Volume = side x side x side = (side)3
To evaluate the volume of a unit cube, we know that the side of a cube is 1 unit. Therefore,
Volume of unit cube = 1 x 1 x 1 = 13= 1
∴ The volume of unit cube = 1 unit3 or 1 cubic unit.
So, the volume of a cube is 1 cubic unit.
Now, let us calculate the surface area of a unit cube.
Surface Area of Unit Cube
A unit cube has 6 faces, and the dimension of each side is 1 unit. All the faces are square in shape.
So, the area of each face = Side x Side
= 1 unit x 1 unit
= 1 square unit
A unit cube has 6 faces of 1 square unit each.
Therefore, the total surface area of unit square = 6 x area of one face of a unit square
= 6 x 1 square unit
= 6 square units
Hence, the surface of the unit cube is 6 square units.
Do You Know?
A unit cube is used to calculate the density of any object. (How much mass an object has of one unit cube is known as the density of any object.)
It is also used to calculate the volume of other cubic or cuboidal objects. (We can calculate it by filling or building the object using the unit cube.)
Numerical Type Questions on Cubes
Question 1. What is the volume of an object that is made up of combining the six unit cubes?
Solution: The new shape is made by combining the six unit cubes.
We know that the volume of a unit cube is 1 cubic unit.
Therefore, the volume of the new object = 6 x 1 cubic unit
= 6 cubic unit
Question 2: What is the density of an object of mass 500 kg which occupies a space of a unit cube?
Solution: We know that the density of an object is equal to the mass of an object occupied by one unit cube.
So, density = $\frac{Mass}{Volume}$
Density = $\frac{500kg}{1 cubic unit}$
Density = 500 kg unit-3
A Tip for Parents
We request all parents to introduce their children to geometrical shapes. Show them daily-life examples of different shapes and their applications. Introducing different shapes not only helps them to learn the concept deeply but also opens further dimensions to increase their quantitative and numerical ability.
Conclusion
In this article, we have learnt about the cube and unit cube. We have also derived the value of the volume and surface area of a unit cube.
To know more about geometrical shapes and key terms, you can visit our website.
FAQs on Understanding Unit Cubes in Geometry
1. What is a unit cube in math?
A unit cube is a cube with side length 1 unit, used to measure volume. It is the basic building block for finding the volume of 3D shapes.
- Each edge measures 1 unit (1 cm, 1 m, etc.).
- Its volume is 1 cubic unit.
- It helps count how many cubic units fill a solid figure.
2. What is the volume of a unit cube?
The volume of a unit cube is 1 cubic unit. Since volume of a cube is given by side × side × side, we calculate:
- Side length = 1 unit
- Volume = 1 × 1 × 1 = 1
3. How do you find volume using unit cubes?
To find volume using unit cubes, count how many cubes fill the solid completely. Each cube represents 1 cubic unit.
- Count cubes in one layer.
- Multiply by number of layers.
- Total cubes = volume in cubic units.
4. What is the formula for counting unit cubes in a rectangular prism?
The number of unit cubes in a rectangular prism is found using length × width × height. This gives the total volume in cubic units.
- Volume = l × w × h
- Example: 5 × 2 × 3 = 30 cubic units
5. Why are unit cubes important in measuring volume?
Unit cubes are important because they provide a standard way to measure volume in cubic units. They help learners visually understand three-dimensional space.
- They show how space is filled.
- They connect counting to volume formulas.
- They form the basis of volume measurement in geometry.
6. What is the difference between a unit square and a unit cube?
A unit square measures area, while a unit cube measures volume. A unit square has side length 1 unit in 2D, while a unit cube has side length 1 unit in 3D.
- Unit square area = 1 square unit.
- Unit cube volume = 1 cubic unit.
- Square → 2 dimensions; Cube → 3 dimensions.
7. How many unit cubes make a cube of side length 3?
A cube with side length 3 units contains 27 unit cubes. Using the volume formula for a cube:
- Volume = side³
- = 3³ = 3 × 3 × 3 = 27
8. Can you give an example of counting unit cubes in a shape?
Yes, for example, a rectangular prism with dimensions 2 × 3 × 4 contains 24 unit cubes. Calculate using:
- Volume = l × w × h
- = 2 × 3 × 4 = 24 cubic units
9. What units are used with unit cubes?
Unit cubes are measured in cubic units such as cm³, m³, or in³. The unit depends on the length measurement used.
- If side is in cm → volume in cm³.
- If side is in m → volume in m³.
- If side is in inches → volume in in³.
10. What are common mistakes when counting unit cubes?
A common mistake when counting unit cubes is forgetting to count hidden or stacked cubes. This leads to incorrect volume calculations.
- Missing cubes in back layers.
- Counting only visible faces.
- Not multiplying by height (number of layers).
