Theorem on the Sum of Opposite Angles of the Cyclic Quadrilateral

In this article, we will prove the theorem and the converse of the theorem on the sum of opposite angles of a cyclic quadrilateral. The Cyclic Quadrilateral Theorem is a fundamental tool of Euclidean Geometry that connects the quadrilateral with the circles and tells us about the properties of cyclic quadrilaterals. In this article, some of the solved examples related to the application of the theorem and the converse of the theorem will also be discussed along with the applications of the theorem in the real world for a crystal clear understanding of the topic.

History of Euclid

Euclid

Name: Euclid

Born:  325 BC

Died:  265 BC

Field: Mathematics

Nationality: Egypt

Statement of the Theorem on the Sum of Opposite Angles of a Cyclic Quadrilateral

According to the Cyclic Quadrilateral Theorem, the sum of either pair of opposite angles in a cyclic quadrilateral is supplementary, i.e., 180 degrees.

Proof of Theorem on Sum of Opposite Angles of Cyclic Quadrilateral

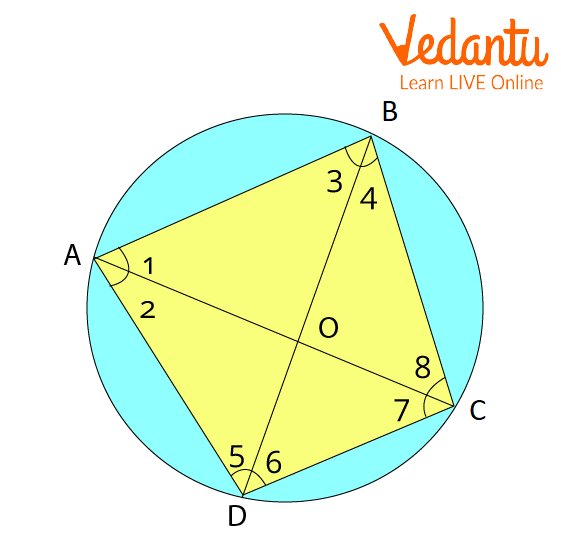
Cyclic quadrilateral ABCD with centre O

Given: Consider a cyclic quadrilateral $A B C D$ in a circle with a centre at $O$.

To prove: $\angle B A D+ \angle B C D=180^{\circ}$

$\angle A B C+ \angle A D C=180^{\circ}$

$A B$ is the chord of the circle.

$\Rightarrow \angle 5=\angle 8$ .. (1) (Angles in the same segment are equal)

$B C$ is the chord of the circle.

$\Rightarrow \angle 1=\angle 6$...(2) (Angles in the same segment are equal)

$C D$ is the chord of the circle.

$\Rightarrow \angle 2=\angle 4 \ldots$... (3) (Angles in the same segment are equal)

$A D$ is the chord of the circle.

$\Rightarrow \angle 7=\angle 3 \quad \ldots$ (4) (Angles in the same segment are equal)

By angle sum property of a quadrilateral,

$\angle A+\angle B+\angle C+\angle D=360^{\circ}$

$\Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 7+\angle 8+\angle 5+\angle 6=360^{\circ}$

$\Rightarrow(\angle 1+\angle 2+\angle 7+\angle 8)+(3+\angle 4+\angle 5+\angle 6)=360^{\circ}$

$\Rightarrow(\angle 1+\angle 2+7+\angle 8)+(-7+\angle 2+\angle 8+\angle 1)=360^{\circ}$

From equations (1), (2), (3), and (4),

$2(\angle 1+\angle 2+\angle 7+\angle 8)=360^{\circ}$

$\Rightarrow(\angle 1+\angle 2+\angle 7+\angle 8)=180$

$\Rightarrow(\angle 1+\angle 2)+(\angle 7+\angle 8)=180^{\circ}$

$\Rightarrow \angle B A D+\angle B C D=180^{\circ}$

Similarly, $\angle A B C+\angle A D C=180^{\circ}$

Hence proved.

The Converse of Cyclic Quadrilateral

Converse of Cyclic Quadrilateral Theorem

Given: ABCD is a quadrilateral with:

$\angle B A C+\angle B D C=180^{\circ}$

$\angle A B D+\angle D C A=180^{\circ}$

To Prove: $A B C D$ is a cyclic quadrilateral.

Proof: Since A, B, C are non-collinear, the circle passes through three collinear points.

Let us draw a circle $C_{1}$ with the centre at $O$.

Let us suppose $D$ does not lie on $C_{1}$. Now,

$\therefore A B C E$ is a cyclic quadrilateral.

But given

$\Rightarrow \angle B A C=\angle B E C=180^{\circ}$

Thus,

$\Rightarrow \angle B E C=\angle B D C$

Now, $\ln \Delta \mathrm{BDE}$,

$\Rightarrow \angle B E C=\angle B D E+\angle D B E$ (Exterior angle Property)

$\Rightarrow \angle B E C=\angle B D C+\angle D B E$

$\Rightarrow \angle B D C-\angle B D C=\angle D B E$

$\Rightarrow \angle D B E=0$

$\therefore$ $E$ and $D$ Coincides

Thus, our assumption was wrong.

$\Rightarrow$ Point $D$ lies on circle $C_{1}$

$\Rightarrow A B C D$ is a cyclic quadrilateral.

Hence proved.

Limitations of the Theorem on the Sum of Opposite Angles of a Cyclic Quadrilateral

• The Cyclic Quadrilateral theorem only tells us about the opposite pair of angles and doesn't tell anything about the corresponding pairs of angles.

• The cyclic quadrilateral is not applicable if any quadrilateral is formed with only three points on the circumference and a fourth point inside the circle.

Applications of the Theorem on the Sum of Opposite Angles of a Cyclic Quadrilateral

• The cyclic Quadrilateral Theorem is used in computer programming.

• It is used in graphic arts, logos, and packaging.

• It is used in making paintings, sculptures, etc.

Solved Examples

1. Find the value of angle D of a cyclic quadrilateral, if angle B is $80^{\circ}$.

ABCD is a cyclic quadrilateral with angle B is 80 degrees.

Ans: Since $A B C D$ is a cyclic quadrilateral,

Hence, the sum of a pair of two opposite angles $=180^{\circ}$.

$\Rightarrow \angle B+\angle D=180$

$\Rightarrow 80^{\circ}+\angle D=180^{\circ}$

$\Rightarrow \angle D=180^{\circ}-80^{\circ}$

$\Rightarrow \angle D=100^{\circ}$

The value of angle $D$ is $100^{\circ}$.

2. Find the value of angle $D$ of a cyclic quadrilateral, if angle $B$ is $120^{\circ}$.
Ans:
As ABCD is a cyclic quadrilateral, hence the sum of a pair of two opposite angles $=180^{\circ}$.

$\Rightarrow \angle B+\angle D=180^{\circ} \\$

$\Rightarrow 120^{\circ}+\angle D=180^{\circ} \\$

$\Rightarrow \angle D=180^{\circ}-120^{\circ} \\$

$\Rightarrow \angle D=60^{\circ}$

The value of angle D is $60^{\circ}$.

3. In the figure given below, $A B C D$ is a cyclic quadrilateral in which

$\angle B A D=100^{\circ}$ and $\angle C D B=50^{\circ}$. find $\angle D B C$ ?

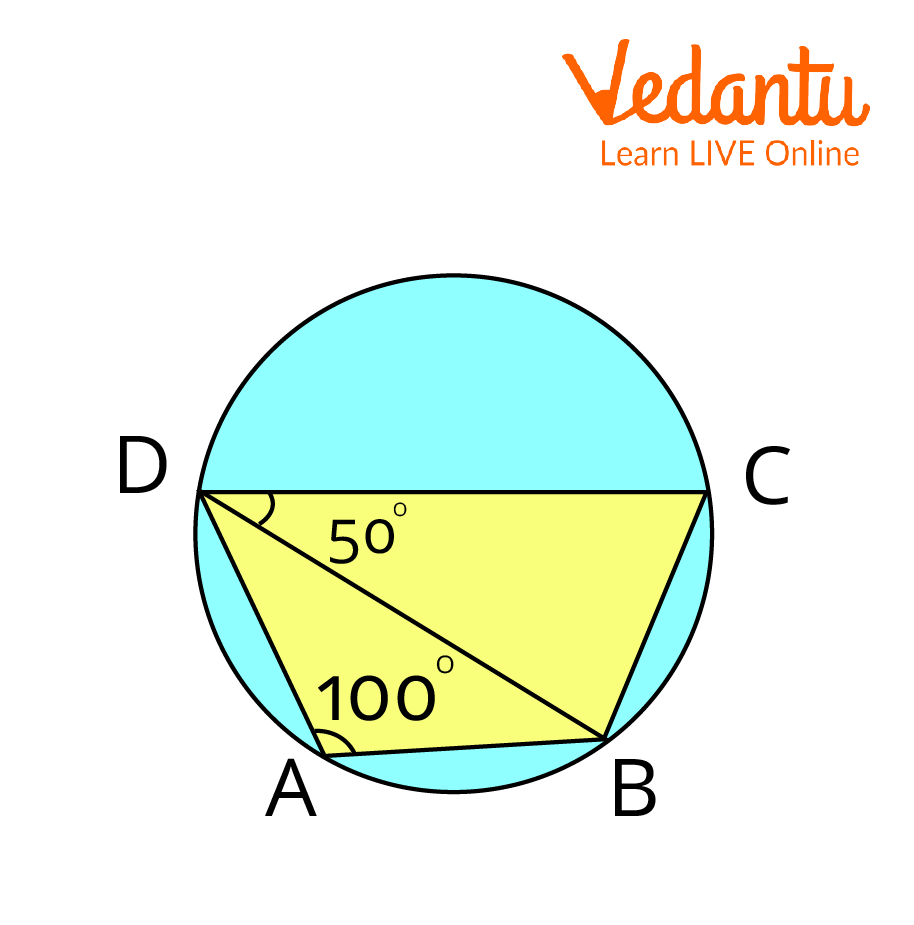
To find angle DBC in a cyclic quadrilateral

Ans:

Given,

$\angle B A D=100^{\circ}$ and $\angle C D B=50^{\circ}$

$\angle B A D+\angle B C D=180^{\circ}$ as these both angles are opposite angles of a cyclic quadrilateral.

$\Rightarrow \angle B C D=180^{\circ}-100^{\circ}=80^{\circ}$

In $\triangle B C D$,
$\angle B C D+\angle C D B+\angle D B C=180^{\circ}$

$\Rightarrow 80^{\circ}+50^{\circ}+\angle D B C=180^{\circ}$

$\Rightarrow \angle D B C=180^{\circ}-130^{\circ}$

$\Rightarrow \angle D B C=50^{\circ}$

Therefore,

$\Rightarrow \angle D B C=50^{\circ}$

Important Points to Remember

• The sum of pairs of opposite angles of a cyclic quadrilateral is always supplementary.

• If the sum of a pair of opposite angles of a Quadrilateral is supplementary, then the quadrilateral is a cyclic quadrilateral.

Important Formulas to Remember

• If $ABCD$ is a cyclic quadrilateral in a circle with centre O, then $\angle B A D+ \angle B C D=180^{\circ}$.

• If in a quadrilateral $ABCD$, $\angle B A D+ \angle B C D=180^{\circ}$, then $ABCD$ must be a cyclic quadrilateral.