Decagon sides formula properties and solved examples
How Many Sides A Decagon Has?
Have you ever wondered what would a shape look like if it had ten sides? We, on our every day life, see different shapes, for example, a window has four sides, a triangle has three sides and a pentagon has five sides. Similarly, a shape having 10 sides is called a decagon. We also define decagon as the polygon having ten sides, ten interior angles, ten exterior angles, and ten vertices.
For example, the shape of a star has 10 sides, 10 vertices, which clearly indicates that the star is a decagon. Various types of decagons we study in mathematics. Here, on this page, we will focus on three types which are regular and irregular decagon, convex and concave decagon, and simple and complex decagon.
Now, let us start with the definition of a decagon and proceed with its formula for finding the number of sides and angles.
What is a Decagon: Definition and Properties
From the above text, we understand that the decagon has all four things like sides, vertices, interior, and exterior angles as 10 in number.
Here, each interior angle is 144° which sums up to 1440° angle.
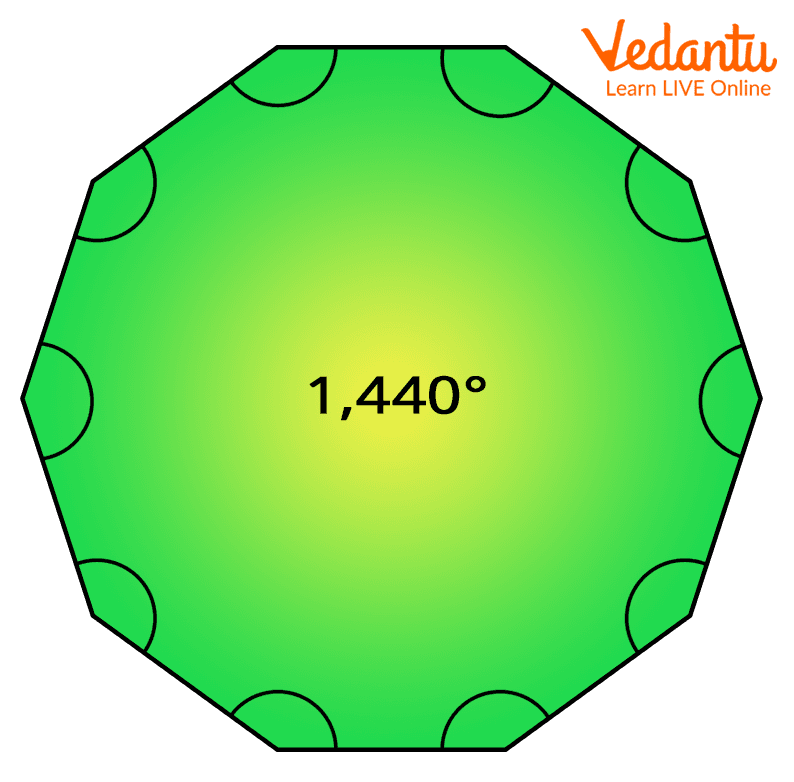
A regular decagon with each exterior angle of 144°
Similarly, each exterior angle is of 36° and angle summing up to 3610 = 360°.
Properties of a Decagon
Below, you can find the important properties of a decagon that will be helpful for you to understand the types of decagons we will be discussing further:
There are 10 sides of a decagon.
The sum of the interior angles is 1440°.
The sum of the measurements of all the exterior angles, i.e., 36 10 is 360°.
The central angle measures 36° (it’s just in the case of a regular decagon).
A decagon shape has 35 diagonals.
There are 8 triangles in a decagon.
Now, let us study the types of decagons with examples.
Types of Decagon
Regular and Irregular Decagon
1. Regular Decagon: A decagon with all its sides equal in length and all the angles equal in measure. In a regular decagon, each interior angle is of 144°, summing to 1440°, while the exterior angles add up to 360°.
The shape of a regular decagon is below:
Regular Decagon
2. Irregular decagon: A decagon that bears irregularity in the length of sides, and measurement of angles is an irregular decagon. The shape of an irregular decagon is shown below:
Irregular Decagon
Convex and Concave Decagon
1. Concave Decagon: Likewise regular and irregular decagons, decagons can be both convex and concave. A concave decagon bulges outward just like you can see in the below image of a concave mirror that you can find in your torch lights, shaving mirror:
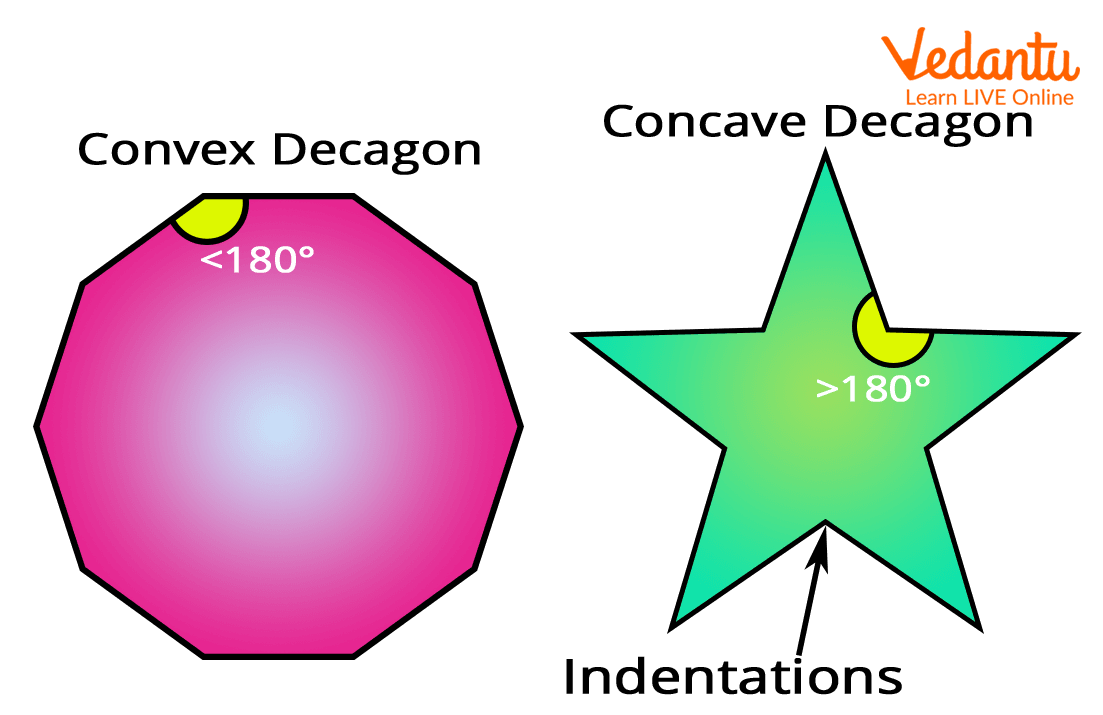
Concave and Convex Decagons
Here, you can see that all the interior angles are less than 180°. Also, at least one of the interior angles is greater than 180° in concave decagons.
Now, let us talk about convex decagons.
2. Convex Decagons: A convex decagon has all the interior angles greater than 180°, which means it is just the reverse of the concave decagon.
Simple and Complex Decagon
Simple Decagon: Simple decagons have no sides crossing themselves. These decagons follow all of the above said regular decagon rules.
Complex Decagon: Complex decagons are self-intersecting and have additional interior spaces. Also, they do not strictly follow any prescribed rules of decagons concerning their interior angles and their sums.
Formula to Find the Number of Sides of a Decagon
We know that the sum of interior angles of a decagon is 1440°. Now, to find the measure of each interior angle, we use the following formula:
Sum of interior angles/number of sides of a decagon (n)
Here, the sum is 1440° and n = 10, so each interior angle is 1440°/10 = 144°.
Also, if we need to find the sum of interior angles, we can use:
Sum of interior angles = (n - 2) 180.
Here, n = 10
So, (10 - 2) 180 = 8 180 = 1440°.
Similarly, to find the number of sides of a decagon, we have:
Sum of interior angles = (n - 2) 180.
1440 = (n - 2) 180
n - 2 = 8
Or, n = 10 sides of a decagon.
So, this was all about the decagon, its shape, number of sides, angles (both interior and exterior), also the formulas to find the number of sides and angles. We also learned the types of decagons that you also find in real life. Understanding formulas on polygons will help you find the sides and angles in any type of polygon.
FAQs on How Many Sides Does a Decagon Have
1. How many sides does a decagon have?
A decagon has 10 sides. A decagon is a polygon with ten straight line segments and ten vertices. Because it has 10 sides and 10 interior angles, it is classified as a 10-sided polygon in geometry. If all sides and angles are equal, it is called a regular decagon.
2. What is the formula for the number of sides in a decagon?
The number of sides of a decagon is 10, based on polygon naming rules and the formula for polygons. In general, the number of sides of a polygon is represented by n. For a decagon:
- n = 10
- It has 10 vertices
- It has 10 interior angles
The prefix “deca-” means ten, which directly indicates the number of sides.
3. What is the sum of interior angles of a decagon?
The sum of the interior angles of a decagon is 1440°. The formula for the sum of interior angles of any polygon is:
- (n − 2) × 180°
For a decagon, n = 10:
- (10 − 2) × 180° = 8 × 180° = 1440°
This applies to both regular and irregular decagons.
4. What is the measure of each interior angle of a regular decagon?
Each interior angle of a regular decagon measures 144°. In a regular polygon, all angles are equal, and each interior angle is calculated using:
- Interior angle = [(n − 2) × 180°] ÷ n
For n = 10:
- [(10 − 2) × 180°] ÷ 10 = 1440° ÷ 10 = 144°
5. How many diagonals does a decagon have?
A decagon has 35 diagonals. The formula to find the number of diagonals in a polygon is:
- n(n − 3) ÷ 2
For a decagon (n = 10):
- 10(10 − 3) ÷ 2 = 10 × 7 ÷ 2 = 70 ÷ 2 = 35
Diagonals are line segments joining non-adjacent vertices.
6. What is the difference between a regular and an irregular decagon?
A regular decagon has all sides and interior angles equal, while an irregular decagon does not. Key differences include:
- Regular decagon: 10 equal sides and each interior angle = 144°
- Irregular decagon: Sides and angles are not all equal
- Both have 10 sides and 1440° total interior angle sum
The structure, symmetry, and angle measures vary only in the irregular case.
7. How do you calculate the perimeter of a decagon?
The perimeter of a decagon is found by adding all 10 sides, or by using Perimeter = 10 × side length for a regular decagon. For example:
- If one side = 6 cm
- Perimeter = 10 × 6 = 60 cm
For an irregular decagon, add the lengths of all ten sides individually.
8. What is the formula for the area of a regular decagon?
The area of a regular decagon is calculated using Area = (5/2) × s² × √(5 + 2√5), where s is the side length. This formula applies only to a regular decagon. Alternatively, you can use:
- Area = (1/2) × perimeter × apothem
Both methods give the same result when the decagon is regular.
9. What is the measure of each exterior angle of a regular decagon?
Each exterior angle of a regular decagon measures 36°. The formula for each exterior angle of a regular polygon is:
- Exterior angle = 360° ÷ n
For n = 10:
- 360° ÷ 10 = 36°
The sum of all exterior angles of any polygon is always 360°.
10. Can you give a real-life example of a decagon?
A common real-life example of a decagon is a ten-sided coin or decorative tile. In architecture and design, regular decagon shapes are used for:
- Floor tiles and patterns
- Gazebo or pavilion layouts
- Coin designs in some countries
These shapes use the geometric properties of a 10-sided polygon for symmetry and balance.
