Sets and Set Difference

In addition to mathematics, sets are used frequently in everyday life. The most practical example of a set is a kitchen. The kitchen is usually well organized by our mother. Kids’ school bags are another example, where you keep all your copies and books. Together make a bag, and we can call it a set. One of the most significant and fundamental sets theory operations is set difference. The difference between two sets, A and B, is another set consisting of elements from A that are NOT in B. In this article, we will learn about the difference of 2 sets and some of the properties of set difference.

Sets

In mathematics, a set is a well-defined collection of objects. Sets are named and represented using capital letters. In set theory, the elements that a set comprises can be any kind of thing: people, letters of the alphabet, numbers, shapes, variables, etc.

From the below image, we can say that there is the P set in which different shapes are there. And it can be termed as subsets.

Pictorial Understanding of Sets

Set Difference

The set operation difference between sets implies subtracting the elements from a set, similar to the difference between numbers. The difference between sets $A$ and $B$, denoted as $A-B$, lists all the elements in set $A$ but not in set $B$. $A-B$ states that elements of $A$ are not the elements of $B$. Therefore, $A - B = \{x : x \in A$, and $x \notin B\}$ and $B-A=\{x: x \in B$, and $x \notin A\}$

Example of AB Sets

So, as far as we have learned, the sets and sets are different. Now let’s see what AB sets are. If A and B are two sets and each element of set A is also an element of set B, then A is referred to as a subset of B.

For example,

Let A = {1, 3, 5}

B = {5, 1, 7, 3}

Here, A is a subset of B.

Since all the elements of set A are contained in set B,

But B is not a subset of A, as all the elements of set B are not contained in set A.

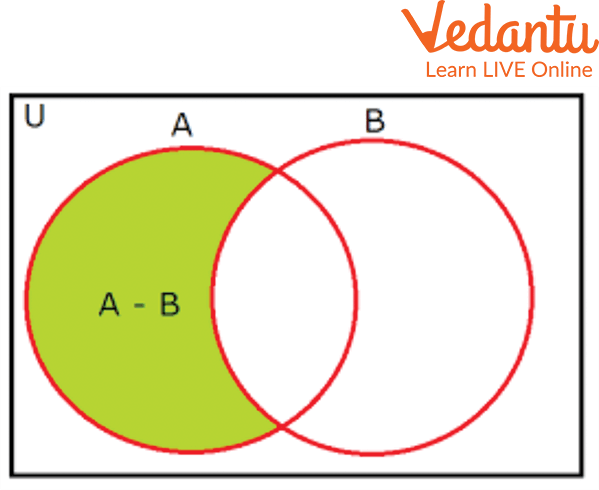
Set Difference

Set Difference Properties

Set difference properties are classified into two categories:

1. The set remains unchanged by the change in the order in which the components are written. Hence, a set {x,y,z} can be write as {y,z,x} or {y,x,z} or {x,z,y} or {z,y,x} or {z,x,y}

For example A={3,6,9}

Similarly, {3,6,9} = {6,9,3} = {3,9,6} = {9,6,3} = {9,3,6}

2. The set remains the same if any element is repeated more than once. To be more precise, repeated elements are considered as a single element, i.e. {1,2,2,2,3,4,4} ={1,2,3,4}

Difference Between 2 Sets

• If A and B are two sets, then to find their difference, it is needed to write in A - B or B - A.

• If A = {2, 3, 4} and B = {4, 5, 6}

A - B describes the elements of A that are not B's elements.

i.e., in the above example, A - B = {2, 3}

In general, A - B = {x : x ∈ A, and x ∉ B}

• If A and B are disordered sets, A - B equals A, and B - A equals B.

An Example of a Set Difference:

Find the differences between 2 sets A-B and B-A, where set A = {1, 2, 3, 4} and set B = {2, 3, 5, 7}

Ans: It is given that A = {1, 2, 3, 4} and B = {2, 3, 5, 7}. Then

A - B = 1, 2, 3, 4- 2, 3, 5, 7 = 1, 4,

B - A = 2, 3, 5, 7-1, 2, 3, 4 = 5, 7

Therefore, A - B = {1, 4} and B - A = {5, 7}

Solved Problems

Q 1. If $A=\{1,2,3,4,5,6\}$ and $B=\{3,4,5,6,7,8\}$, then find $A-B$ and $B-A$.

Ans: From the given question, we have the sets given as

$A=\{1,2,3,4,5,6\}$

$B=\{3,4,5,6,7,8\}$

Now finding the A - B and B - A.

$A-B=\{1,2\}$ since the elements 1,2 are there in $A$ but not in $B$.

Similarly,

$B-A=\{7,8\}$, since the elements 7 and 8 belong to $B$ and not to $A$.

Q 2. If $X=\{11,12,13,14,15\}, Y=\{10,12,14,16,18\}$ and $Z=\{7,9,11,14,18,20\}$, then find the following:

(i) $X-Y-Z$

Ans: From the given question, we have the sets given as

$X=\{11,12,13,14,15\}$

$Y=\{10,12,14,16,18\}$

$Z=\{7,9,11,14,18,20\}$

$X-Y-Z=\{11,12,13,14,15\}-\{10,12,14,16,18\}-\{7,9,11,14,18,20\}$ $=\{13,15\}$

(ii) $Y-X-Z$

Ans:$Y-X-Z=\{10,12,14,16,18\}-\{11,12,13,14,15\}-\{7,9,11,14,18,20\}$ $=\{10,16\}$

Practice Questions

Q 1. Find the differences between sets $A-B$ and $B-A$, where set

$A=\{1,2,3,4\} \text { and set } B=\{2,3,5,7\}$

Ans: $A-B=\{1,4\}$ and $B-A=\{5,7\}$

Q 2. Let set A = {1, 2, 4, 5, 6, 7, 9}, and set B = {3, 4, 6, 7, 9} Find A - B.

Ans: A - B={1, 2, 5}

Summary

A set is a mathematical representation of a collection of various items. It contains elements that may be any type of mathematical object. A set is always defined as a term surrounded by curly brackets. The term “set difference” subtracts one set from another. A subtraction symbol between two sets defines the difference between the sets, i.e., (A-B). The set remains the same if the order of data inside the brackets is changed, and the set value remains the same if any number comes more than once.