




What Sets Probability Apart from Likelihood?
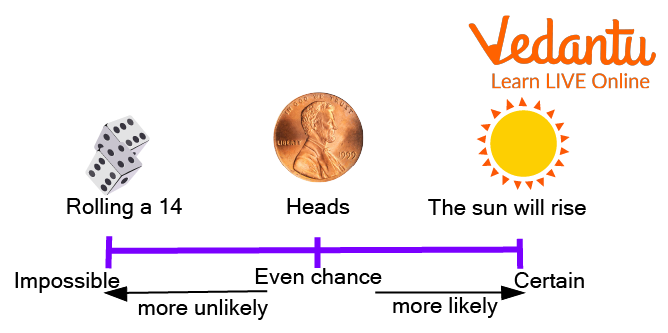
The likelihood is the condition of being likely or probable; the probability of a chance or a probability of something. Example: There is a strong likelihood of him being the class monitor. The probability of an event is a number telling the possibility that the event will happen. An event that is sure to occur has a probability of 1.
An event that possibly cannot occur has a probability of zero. If there is a possibility that an event can occur or not, then its probability is between zero and 1. In this article, we will see the terms related to probability.

Probability chart
What is Probability?
Probability defines the likelihood of the occurrence of an event. Probability can be defined as the ratio of the number of favorable outcomes to an event's total number of outcomes. Probability generally has great applications in games and in business to make probability-based predictions, and also, probability has extensive applications in this new area of artificial intelligence.
Terms Related to Probability
Following are some of the terms related to probability:
Experiment- A process that can deliver some well-defined results is called an experiment. Each outcome is known as an event.
Random Experiment- In an experiment where all probable results are known in advance, but the exact result cannot be predicted is known as a random experiment.
Thus, when we toss a coin, we know all possible outcomes: Heads or Tails.
Though, when we toss a coin randomly, we cannot foresee in advance whether it will be a head or a tail.
So, tossing a coin is a random experiment.
Likewise, tossing a die is also a random experiment.
Trial- Through a trial, we understand conducting a random experiment.
For instance:- Tossing a dice or tossing a coin etc.
Probability of Happening of an Event- The probability of happening of an event can be defined as $P$ (happening of an event) $=E_2$ (Number of trials in which the event successfully happened.) divided by $E_1$ (the total number of trials.)
$P=\dfrac{E_2}{E_1}$.
What is Likelihood?
Things that will certain to happen i.e. if you mean something is likely to happen, and you give the idea that no matter what plot you come up with to wind things around but it will still happen sooner or later.
Difference Between Sure and Impossible Event
Following is the difference between a sure and impossible event:
Types of events
Real-Life Example of Probability
Probability in day-to-day life, we come across mentions such as
Most probably, it will be sunny today.
Chances are high that the prices of diesel will go up.
I doubt that he will win the match.
The words ‘most probably’, ‘chances,’ ‘doubt’, etc., indicate the probability of happening an event.
Fun Activity
Tell whether the given below is certain to occur, impossible to occur, or can occur but not certain.
(i) You are older today than yesterday.
(ii) A tossed coin will land with heads-up.
(iii) A dice, when tossed, shall land up with 9 on top.
(iv) The next traffic light seen will be yellow.
(v) Tomorrow will be a rainy day.
Make your Guess.
Ans:
i) Certain to happen.
ii) It can occur but not certain.
iii) Impossible
iv) It can occur but not certain.
v) It can occur but not certain
Solved Examples
Q 1. There are 6 cushions in the bed. 3 are yellow, 2 are red, and 1 is green. What is the probability of picking a red cushion?
Ans: The probability is = to the number of red cushions divided by the total number of cushions, that is $\dfrac{2}{6} = \dfrac{1}{3}$.
Q 2. There is a box full of colored jars, red, blue, green, and orange. Some of the jars are picked out and displaced. Aditi did this 1000 times and reached the given results:
Number of blue jars picked out: 300
Number of red jars: 200
Number of orange jars: 450
Number of green jars: 50
What is the probability that Aditi will pick a green jar?
Ans: For every 1000 jars picked out, 450 are orange.
Therefore, P(orange) = $\dfrac{450}{1000}$
= 0.45
Practice Questions
Q 1. In a toss of a coin, what is the probability of getting a head?
Ans: $\dfrac{1}{2}$
Summary
The probability of an event occurring is defined by likelihood. The outcome of an event may be sure or not sure to us. When this happens, we say there is a chance that the event will happen. In this article, we saw how Probability plays an important role in everyday life. Even in sports and gaming strategies, weather forecasts, selling or buying insurance, online shopping, online games, checking blood groups, and analyzing political strategies. With the right sense of probability leading, life can be easier. So it is necessary to learn the basic concept of probability.
FAQs on Probability vs Likelihood Explained for Students
1. What are the types of probability?
Four types of probability are commonly used:
Classical, Empirical, Subjective, and Axiomatic.
2. Who founded mathematical probability?
A gambler's quarrel in 1654 led to the invention of a mathematical theory of probability by two renowned French mathematicians, Blaise Pascal and Pierre de Fermat.
3. How was probability discovered?
The word probability started in the seventeenth century when it referred to actions or opinions that sensible people held. Further, the word probable in the legal content referred to a proposition with tangible proof. The field of permutations and combinations, statistical inference, cryptoanalysis, and frequency analysis have contributed to this current field of probability.























