Finding the Prime Factorization of 729

What is the prime factorization of 729? Are you aware of it? In this article, we will learn how to compute factors of 729, prime factors of 729, and factors of 729 in pairs, as well as solve examples for better understanding. The numbers that when multiplied together result in the number 729 are called factors of 729. For instance, when we multiply 3 and 4, we get 12, which means that $3\times 4$ and that 3 and 4 are factors of 12. Read ahead to learn more about the prime factorization of 729.

All Factors of 729

The number 729 is a perfect cube. Factors of 729 are the numbers that divide 729 exactly with no remainder. When you multiply two whole numbers together and obtain 729 as the result, you may claim that both numbers are factors of 729. As a result, the factors of 729 are 1, 3, 9, 27, 243, and 729.

How to Find the Factors of 729?

To identify the factors of 729, first, we need to generate a list of numbers that divide 729 without leaving a remainder.

$729\div 1=729$

$729\div 3=243$

$729\div 9=81$

$729\div 27=27$

$729\div 81=9$

$729\div 243=3$

$729\div 729=1$

As a result, the factors of 729 are 1, 3, 9, 27, 81, 243, and 729.

Prime Factorization Method

Prime factorization method is defined as the process of determining a number’s prime factors so that the original number is evenly divided by these factors because a composite number includes more than two factors. Thus, this method applies only to composite numbers instead of prime numbers.

A few examples of the prime factorization are as follows:

9 is $3\times 3$

14 is $2\times 7$

Prime Factorization of 729 by Division Method

Prime factors are prime numbers that can equally divide the original integer. To get the prime factorization of 729, divide 729 by prime numbers until the quotient is 1.

Step 1: Divide 729 by 3.

$729\text{ }\div \text{ }3\text{ }=\text{ }243$

Step 2: Again divide 243 by 3.

$243\text{ }\div \text{ }3\text{ }=\text{ }81$

Step 3: Divide 81 by 3.

$81\text{ }\div \text{ }3\text{ }=\text{ }27$

Step 4: Continue with the prime number, i.e., 3.

$27\text{ }\div \text{ }3\text{ }=\text{ }9$

Step 5: Again, divide 9 by 3.

$9\text{ }\div \text{ }3\text{ }=\text{ }3$

Step 6: Divide 3 by 3.

$3\text{ }\div \text{ }3\text{ }=\text{ }1$

Thus, we get 1 at the end of this division method, and we can’t go on with the division approach. Hence, the prime factorization of 729 is $3\times 3\times 3\times 3\times 3\times 3$ or ${{3}^{6}}$ where 3 is a prime number.

Factor Tree of 729

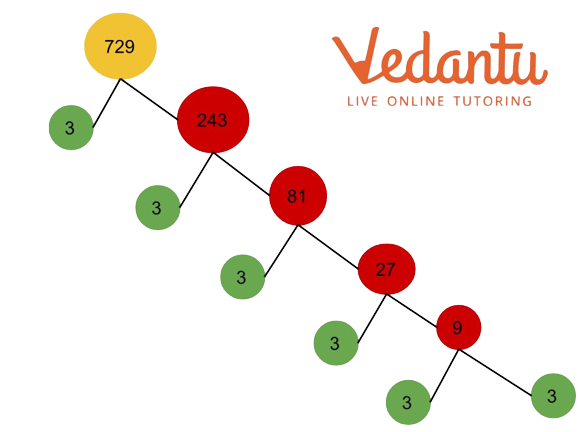
Factor Tree of 729

Pair Factors of 729

When multiplied in pairs, the numbers that provide the original number, 729, are known as 729's pair factors. The pair factors of 729 might have both positive and negative values.

Thus, the positive pair factors are $\left( 1,\text{ }729 \right),\text{ }\left( 3,\text{ }243 \right),\text{ }\left( 9,81 \right)$ and $\left( 27,\text{ }27 \right)$.

Thus, the negative pair factors are $\left( -1,\text{ }-729 \right),\text{ }\left( -3,\text{ }-243 \right),\text{ }\left( -9,\text{ }-81 \right)$, and $\left( -27,\text{ }-27 \right)$.

Interesting Facts

• If (a, b) is a number's pair factor, then (b, a) is also a number's pair factor.

• 729 is a perfect cube.

• 1 is the factor for each number, as 1 times a number is the number itself. Again, anything divided by 1 is the number itself.

Solved Important Questions

1. What is the common factor of 129 and 179?

Ans: Write down the factors of 129 and 179.

The factors of 129 are 1, 3, 43, and 129.

The factors of 729 are 1, 3, 9, 27, 243, and 729.

Hence, the common factors of 129 and 179 are 1 and 3.

2. What is the prime factorization of 729?

Ans: Two steps help us to find 159's factors. They are as follows:

Step 1: Write the number 55, which has to be factored in.

Step 2: Find the two numbers whose product is 159.

Consider the integers 3 and 53 to be the two factors. In this case, 3 and 53 are prime numbers that cannot be divided further.

So, 159 is expressed as the product of $3\times 53$.

Thus, the prime factor of 159 is 3x53, where 3 and 53 are prime numbers.

3. Write all factors of 729.

Ans: When you multiply two whole numbers together and obtain 729 as the result, you may claim that both numbers are factors of 729. As a result, the factors of 729 are 1, 3, 9, 27, 3243, 729 and the prime factorization of 729 is $3\times 3\times 3\times 3\times 3\times 3$ or ${{3}^{6}}$ where 3 is a prime number.

Conclusion

This article summarises the prime factorization of 729, all the factors of 729 and pair factors of 729. We now know that the factors of 729 are 1, 3, 9, 27, 243, 729 and the prime factorization of 729 is $3\times 3\times 3\times 3\times 3\times 3$ or ${{3}^{6}}$ where 3 is a prime number. The positive and negative pair factors are $\left( 1,\text{ }729 \right),\text{ }\left( 3,\text{ }243 \right),\text{ }\left( 9,81 \right),\text{ }\left( 27,\text{ }27 \right)$ and $\left( -1,\text{ }-729 \right),\text{ }\left( -3,\text{ }-243 \right),\text{ }\left( -9,\text{ }-81 \right),\text{ }\left( -27,\text{ }-27 \right)$, respectively.

Practice Questions

1. Is 729 a perfect square or cube?

1. Square

2. Cube

2. How many factors does 729 have?

1. 4

2. 5

3. 6

4. 8

Answers:

1) B

2) C