Perpendicular Distance of a Point From a Line

The shortest distance between a point and a line in geometry is the distance of a point from a line. There are an endless number of lines that can be drawn in a plane from one point to another. Drawing a perpendicular line segment on the line passing through the specified location is the only way to get the shortest distance. This is so that we can create a triangle by connecting the point and line with more than one line. Knowing the distance from a point to a line can be useful in various real-life situations-for example, to find the distance between two objects like two trees. In this article, we will study how to find the length of a perpendicular from a point to a line and solved examples.

Perpendicular Distance

The distance between two objects measured along a line perpendicular to one or both is referred to as the perpendicular distance in geometry. In two- dimensional space, the distance between two points and two lines is the perpendicular distance. For the perpendicular distance from the origin to a plane in three dimensions, the point on the plane closest to the origin.

Distance between a point and a plane in three dimensions, for the perpendicular distance between any two points.

Perpendicular Distance of a Point from a Line

The length of the perpendicular drawn from a point to a line represents the shortest separation between the two. The stages to get at the formula for calculating the perpendicular distance of a point from a line are listed below.

Step 1: In the first step, think about a line $L: A x+B y+C=0$ that is $d$ distance from the point $P\left(x_{1}, y_{1}\right)$

Step 2: As illustrated in the diagram below, draw a perpendicular PM from point $P$ to line L.

Step 3: Assume that $Q$ and $R$ are the points where the line intersects the $x, y$ - axis respectively.

Step 4: The point coordinates can be expressed as

$Q\left(\dfrac{-C}{A}, 0\right), R\left(0, \dfrac{-C}{B}\right)$

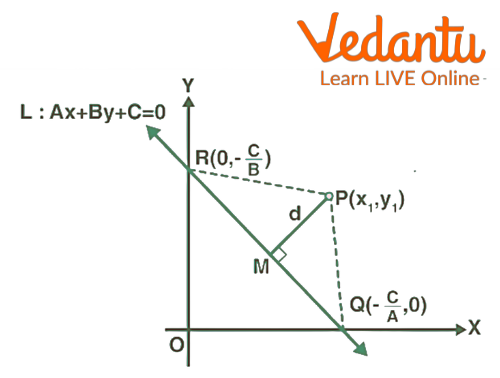
Point Coordinates

Perpendicular Distance Formula

We have the line Ax+By-C-0 i.e. DE and has a slope $\dfrac{-A}{B}$

Perpendicular Distance

Now, we have the point $\mathrm{P}$ as $\left(H^{\prime} H\right)$. So, we have to find a perpendicular distance from $\mathrm{P}$ to DE.

So, construct a line that is parallel to $D E$ and has a slope $\dfrac{-A}{B}$ as it is parallel to DE and then name it FG.

Now, we have to construct line $\mathrm{PQ}$ which passes through the origin and this line is parallel to slope $\dfrac{B}{A}$ as it is perpendicular to DE named as RS then extend it at $(0,0)$.

Slope

As FG has slope $\dfrac{-A}{B}$ and equation we have

$y-n=-\dfrac{A}{B}(x-m)$

$y=\dfrac{-A x+A m+B n}{B}$

We have

$y=\dfrac{B}{A} x$

$\dfrac{B}{A} x=\dfrac{-A x+A m+B n}{B}$

Prove that point $\mathrm{R}$ is $\left(\dfrac{A(A m+B n)}{A^{2}+B^{2}}, \dfrac{B(A m t+B n t)}{A^{2}+B^{2}}\right)$

$y=\dfrac{B}{A} x, A x+B y+C=0$

Implies $y=\dfrac{A x+C}{B}$

$=\dfrac{A x+C}{B}-\dfrac{B}{s} x$

$x=\dfrac{-A C}{A^{2}+B י}$

$y=\dfrac{B}{A} x$

$y=\dfrac{B}{A}\left(\dfrac{A C}{A^{2}+B^{2}}\right)=\dfrac{B C}{A^{2}+B^{2}}$

So, $\mathrm{S}$ is $\left(\dfrac{-A C}{A^{2}+B^{2}}, \dfrac{-B C}{A^{2}+B^{2}}\right)$

$d=\sqrt{\left(\dfrac{-A C}{A^{2}+B^{2}}-\dfrac{A(A m+B n)}{A^{2}+B^{2}}\right)^{2}+\left(\dfrac{-B C}{A^{2}+B^{2}}-\dfrac{B(A m+B n)}{A^{2}+B^{2}}\right)}$

Thus, distance RS is

$=\sqrt{\dfrac{\{-A(A m+B n+C)\}^{2}+\{-B(A m+B n+C)\}^{2}}{\left(A^{2}+B^{2}\right)^{2}}}$

$=\sqrt{\dfrac{\left(A^{2}+B^{2}\right)(A m-B n+C)^{2}}{\left(A^{2}+B^{2}\right)^{2}}}$

$=\sqrt{\dfrac{(A m+B n+C)^{2}}{A^{2}+B^{2}}}$

$=\dfrac{|A m+B n+C|}{\sqrt{A^{2}+B^{2}}}$

Thus, perpendicular distance formula is $d=\dfrac{|A m+B n+C|}{\sqrt{A^{2}+B^{2}}}$

If the perpendicular distance of point P is 5 units away from the axis perpendicularly and the foot of the perpendicular is in the opposite direction of the x-axis then point P has an ordinate which is 5 or -5. As y- coordinate of a point is equal to its perpendicular distance from the x-axis. The perpendicular distance of point P lies on the X-negative axis direction.

The point P therefore has a y-coordinate of 5 or -5.

Length of the Perpendicular from a Point to a Line

Step 1: We have a line $L: A x+B y+C=0$ that is ' $\mathrm{d}$ ' distance from the point $P\left(x_{1}, y_{1}\right)$

Step 2: As illustrated in the diagram below, draw a perpendicular PM from point $P$ to line L.

Step 3: Assume that Q and R are the points where the line intersects the x-axis and y-axis respectively i.e. the length of the perpendicular from a point to a line.

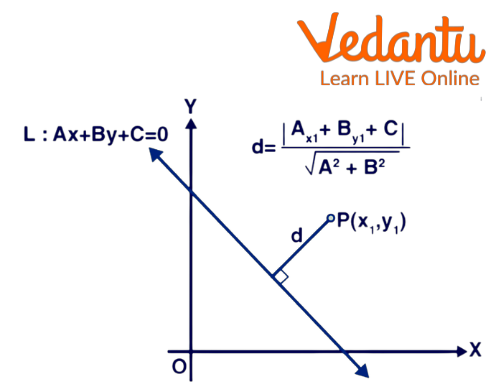
Length of the Perpendicular from a Point to a Line

Solved Examples

Q 1. Locate the distance between the point (-3, 5) and the line 4x - 3y - 26 = 0.

Ans: We have 4x-3y-26 = 0 at (-3, 5)

Implies A = 4, B = -3, C = -26, x = -3, y = 5

$d=\dfrac{|A x+B y+C|}{\sqrt{A^{2}+B^{2}}}$

$d=\dfrac{|4(-3)+(-3) 5+(-26)|}{\sqrt{4^{2}+(-3)^{2}}}=\dfrac{|-53|}{\sqrt{25}}=\dfrac{53}{5}$

Q 2. A line y = 3x + 1 and a point (5,1) must be separated by this distance.

Ans: We have y = 3x+1 at (5, 1)

Implies A = 3, B = -1, C = 1, x = 5, y = 1

$d=\dfrac{|A x+B y+C|}{\sqrt{A^{2}+B^{2}}}$

$d=\dfrac{|3.5+(-1) 1+1|}{\sqrt{3^{2}+(-1)^{2}}}=\dfrac{15}{\sqrt{10}}$

Practice Questions

Q 1. Determine the length of the perpendicular that connects the point (3,2,1) to the line.

Ans: $\dfrac{x-7}{-2}=\dfrac{y-7}{2}=\dfrac{z-6}{3}$

Q 2. Using the formula for the distance of a point from a line, determine the distance between the point K(3,7) and the line PQ.

Ans: $y=\dfrac{6}{5} x+2$

Q 3. Find the perpendicular distance of the point (−1,1) from the line 12(x+6)=5(y−2).

Ans: 5 units

Summary

As we know, the perpendicular distance between a point and a line is the shortest distance. Let that distance be ' $\mathrm{d}$ ' between $P\left(x_{1}, y_{1}\right)$ and line $L: a x+b y+c=0$ as $D=\dfrac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}$

By calculating the perpendicular distance between any point on the line and the other, we may determine how far apart two parallel lines are from one another.