




How to Calculate the Perimeter of a Trapezium Step by Step
Have you ever seen a trapezium shape in your daily life?

Is it Trapezium?
Can you mention a few examples of trapezium or trapezoid? Have a look at your surroundings and decide on the shape of a trapezium. Would you be able to find out any? A little bit confused between trapezium or trapezoid? No worries, you’ll learn the same here. Firstly, trapezium and trapezoid are the same in American and Canadian English, a trapezoid is a quadrilateral with at least one pair of parallel sides. A trapezoid is known as a trapezium in British and other forms of English.
Trapezium
A trapezium is a quadrilateral with one pair of parallel opposite sides, as defined by Euclidean geometry. Trapezium comes from the Greek word "trapeza," which means "table." So, the Trapezium is a four-sided shape with only two parallel sides.
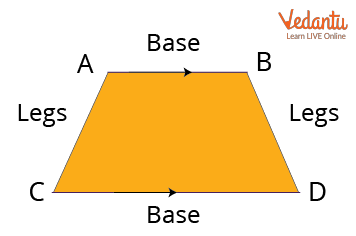
Trapezium
A trapezium is a two-dimensional quadrilateral with a pair of parallel opposite sides (because of its four straight lines). The base and the non-parallel sides of the trapezium are referred to as the base and legs of the trapezium, respectively.
It has four sides and four corners and is a closed plane shape. The following is a diagram of a trapezium shape:
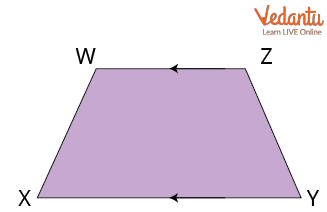
Trapezium WXYZ
In the above figure, XY and WZ are the bases while XW and YZ are the legs of the trapezium.
Properties of a Trapezium
Each quadrilateral has its unique set of characteristics that distinguish it from the other. These attributes provide extra information about a shape's geometrical construction. The following are the properties of trapezium:
It's a two-dimensional shape.
A trapezium's bases are parallel to one another.
A trapezium's diagonals are always intersected by each other.
The total of the adjacent internal angles is 180°.
In a trapezium, the sum of all internal angles is always 360°.
Trapezium Formula
Consider a trapezium with the lengths of parallel sides a and b units and the altitude "h."
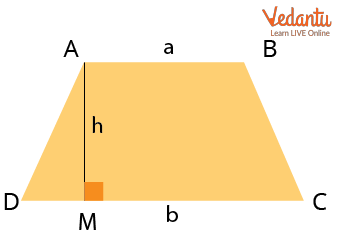
Trapezium with the Lengths of Parallel Sides and the Altitude
Calculating the average of bases and multiplying the result by the altitude yields the trapezium area. As a result, trapezium area $= \left(\dfrac{AB + DC}{2}\right) AM = \left(\dfrac{a+b}{2}\right) h$, where AB, CD represent the bases and AM represents the altitude.
The perimeter of a trapezium is calculated by adding all of its sides together (because the perimeter is the sum of boundaries). As a result, the perimeter of a trapezium ABCD = AB + BC + CD + AD.
Solved Examples
1. If a trapezium is given with its three sides whose measures are 10cm, 12cm, and 7cm. Find the length of the fourth side of the trapezium if the perimeter is 40 cm.
Ans: Perimeter of trapezium = Sum of all its sides (all four sides) = 40 cm
Let the fourth side be ‘a’ cm.
Thus, applying the formula:
Perimeter is 40 = 10 + 12 + 7 + a
a = 40 – (10 + 12 + 7)
a = 40 – 29
a = 11 cm
Therefore, the length of the fourth side is 11 cm.
2. Seeta bought a trapezium-shaped table whose bases and legs are 25 cm,20 cm, 10 cm, and 12 cm respectively. She wants to know the perimeter of the table. Can you help her to find it?
Ans: Perimeter of trapezium = Sum of all its sides
So, applying the formula:
Perimeter of trapezium = 25 + 20 + 10 + 12
Perimeter of trapezium = 67 cm
Hence, the perimeter of the table is 67 cm.
Practice on your own:
Q1. The parallel sides of a trapezium are 25 cm and 11 cm, while its nonparallel sides are 15 cm and 13 cm. Find the perimeter of the trapezium.
Ans: 64 cm
Q2. What is the perimeter of the trapezoid in which the sum of lengths of non-parallel sides is 12 units, and the sum of the parallel sides is 8 units?
Ans: 20 units
Conclusion
Trapezium comes from the Greek word "trapeze," which means "table." So, the Trapezium is a four-sided shape with only two parallel sides. The perimeter of a trapezium is calculated by adding all of its sides together (because the perimeter is the sum of boundaries). As a result, the perimeter of a trapezium ABCD = AB + BC + CD + AD.
FAQs on Perimeter of a Trapezium: Definition, Formula & Examples
1. What is the formula for the perimeter of a trapezium?
The formula for the perimeter of a trapezium is the sum of the lengths of all its sides. If the lengths of the four sides are $a$, $b$, $c$, and $d$, then the perimeter $P$ is:
$$P = a + b + c + d$$
This straightforward equation allows you to find the total boundary length of any trapezium, as taught in Vedantu’s math classes.
2. What is a formula for trapezium?
A trapezium (also known as a trapezoid in some countries) has two key formulas: one for area and another for perimeter.
- Perimeter: $P = a + b + c + d$ (sum of all four sides)
- Area: $A = \frac{1}{2} \times (a + b) \times h$, where $a$ and $b$ are the lengths of the parallel sides and $h$ is the height
3. Is a trapezoid the same as a trapezium?
The terms trapezoid and trapezium can differ by region.
- In British English (and Indian curriculum), a trapezium has exactly one pair of parallel sides—what Americans call a "trapezoid."
- In American English, "trapezium" refers to a quadrilateral with no parallel sides.
4. Is the trapezium perimeter formula complex?
No, the perimeter formula for a trapezium is not complex. It simply involves adding all four side lengths together:
$$P = a + b + c + d$$
Vedantu’s expert teachers make learning such geometric formulas easy with step-by-step guidance and examples.
5. How do you calculate the perimeter of a trapezium with only two parallel sides and two non-parallel sides known?
To calculate the perimeter of a trapezium when you know the lengths of both parallel sides ($a$ and $b$) and both non-parallel sides ($c$ and $d$), simply add all the side lengths:
$$P = a + b + c + d$$
This direct approach is used frequently in Vedantu’s study material and live doubt-solving sessions.
6. What units are used for the perimeter of a trapezium?
The perimeter of a trapezium is always measured in linear units such as meters (m), centimeters (cm), or millimeters (mm), depending on the units given for each side. Vedantu’s teachers always emphasize the importance of consistent units when solving perimeter problems.
7. Does the perimeter formula change for an isosceles trapezium?
No, the perimeter formula for an isosceles trapezium remains
$$P = a + b + c + d$$
The difference is that the non-parallel sides (legs) are equal in length for an isosceles trapezium ($c = d$), which can simplify calculations—a concept reinforced in Vedantu's math curriculum.
8. Why is understanding the perimeter formula important for trapezium exam questions?
Understanding the perimeter formula for trapezium is important because:
- It helps solve geometry questions quickly in school exams.
- It's crucial for solving real-life problems relating to fencing, borders, or construction projects involving trapezium shapes.
- Knowledge of formulas builds foundational skills for more advanced topics, all emphasized and practiced at Vedantu.
9. Can you use the perimeter formula for other quadrilaterals?
Yes, the perimeter concept applies to all quadrilaterals: add up the lengths of all four sides. However, specific names—like trapezium or rectangle—help determine if other formulas (for area, angles, etc.) might be useful. Vedantu’s courses teach when to use each formula based on the shape given.
10. Where can students practice problems on the perimeter of a trapezium online?
Students can practice perimeter of trapezium problems on Vedantu’s online learning platform, which offers
- Interactive quizzes
- Practice worksheets
- Live doubt-clearing sessions























